最近データを統計処理している関係で,統計の話題が多くなる.今回はデータが正規分布しているかどうかの検定について.
正規分布しているかどうかが,なぜ重要なのか?
統計学的検定には,データが正規分布していることを前提にしている場合が多い.だが,実際には正規分布しているデータはあまり多くない.特に,収入などの経済活動においてはべき分布など偏っていることのほうが多い.正規分布を前提に検定を行うと,誤った結論を導くことになりかねない.これは政策決定において決定的な誤りを犯す原因になるのだが,なぜかあまり重要視されていない.
かくいう俺も統計を系統立てて学んだわけではない.ただ,相関係数を求める際に Pearson 相関係数を用いるべきか,Spearman 相関係数を用いるべきか判断に迷った際の基準が欲しかった.
そもそも,正規分布とは?

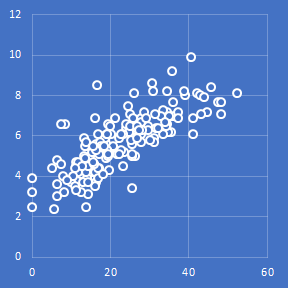
数学的な定義はさておき,左右対称の棒グラフ,と覚えておけば良い.上の図は実際に扱っているデータの度数分布表を作成したものだ.まあ左右対称と言っていいのではないだろうか.こういうデータには Pearson 相関係数を使ってよい.
べき分布など,正規分布でないデータとは?

一方,ふたつ目の図はべき分布の例である.こういうデータは煮ても焼いても食えない.対数変換などの方法もあるらしいが,素直に Spearman 相関係数(順位相関係数ともいう)を用いるべきである.
検定の前に,データの分布を見よう
大事なことなのでもう一度書く.統計学的検定の前に,必ずデータの分布を見よう.その検定法,正規分布を前提にしたものではないか?正規分布していないデータを当てはめて大丈夫なのか?
形を見るだけで不安なら,正規性の検定をしよう
ここからは SPSS を前提に話を進める.データセットのファイルはすでに開いているものとする.
SPSSで正規性検定を行う
メニューから「分析」「記述統計」「探索的…」と進み,ダイアログを開く.

対象の変数を「従属変数」に入れる
対象とする変数を左のパネルから右上の「従属変数」に入れる.一つだけでなく,いくつも選べる.「因子」や「ケースのラベル」はとりあえず無視.


「作図…」ボタンをクリック
右上に「作図…」ボタンがあるのでクリック.「探索的分析:作図」ダイアログが開く.「正規性の検定とプロット」にチェックを入れる.

「続行」をクリックしてダイアログを抜ける.
OKをクリックすると検定が行われる
下図は検定結果の一部分を切り抜いたもの.三段目の「正規性の検定」が重要である.「Kolmogorov-Smirnow の正規性の検定」の中の「有意確率」の数値が重要だ.

有意確率が 0.05 未満なら「正規分布ではない」
この有意確率が 0.05 未満である場合は「正規分布ではない」ということである.こういう場合,厳密には Pearson 相関係数は使えない.Spearman 順位相関係数を用いるべきである,ということになる.
実際には Pearson 相関係数でやっつけてしまうことも多いんだけどね.