収縮に関与する蛋白質はこれまでアクチンとミオシンとされてきた.しかし最近,伸張性収縮(エキセントリック,ネガティブ)様式においてタイチンの果たす役割が明らかになりつつある.今回はタイチンについて述べた論文を紹介する.
訳に揺れが見られるがご容赦を.新規の分野の翻訳には気を使う.’winding filament’ は無理に訳すと「巻きつきフィラメント」とでもなるだろうが,おそらく英語のままにしておいた方が定着しやすいだろう.この用語については山本義徳氏が著書において言及している.
筋収縮の際にアクチンとミオシンが ATP を消費して動力を発生させることはよく知られており,これをフィラメント滑走説という.実は数十年前からこれ以外にも弾性線維の存在を示唆する実験結果が得られており, ‘elastic filament’ と呼称されていたが,フィラメント滑走説で多くの人が納得してしまい,研究は細々としか続いていなかった.
一方,トレーニーの間ではポジティブ収縮よりもネガティブ収縮の方が重い重量を扱えることが経験的に分かっていたが,フィラメント滑走説ではこの矛盾を説明できなかった.
自動車に例えてみよう.エンジンの回転はシャフトを通じてギヤボックスに伝達される.アクチンとミオシンはエンジンとギヤボックスのセットである.そして,エンジンもミオシンも,一方向にしか動力を発生できない.これはギヤボックスにローギヤしか搭載しておらず,リバースギヤが存在しないのと同じである.そんな車はバックができない!ネガティブ収縮とは,高速道路を走っている最中にギヤをリバースに入れるようなものである.オートマ車はそもそもギヤがリバースに入らないよう安全装置が組み込まれているが,マニュアル車ならあっという間にクラッチが焼き付いてエンストしてしまう.
フィラメント滑走説ではミオシン頭部のパワーストロークはポジティブ収縮の際にしか動力を発生できないはずであるが,実際にはネガティブ収縮の時にも動力は発生しており,しかもネガティブ収縮の方が出力が大きい.では,その動力源は何なのか?そしてこの差分の動力はどこから来ているのか?
電子顕微鏡による観察では,ミオシンの末端はフリーではなく, Z 盤に繋ぎ止める蛋白質の存在が指摘されており弾性フィラメントとして機能しているに違いないと言われてきた.この蛋白質は Y 字型をしているため免疫グロブリン (Ig) と表現されるが,もちろん形質細胞から分泌される本物の免疫グロブリンではない.そもそも大きさが全く違う.本物の免疫グロブリンの分子量はたった 25,000 だが,今話題にしているタイチンは 370 万もある.
電子顕微鏡の解像度は理論上は 0.1 nm とされているが,真空中で撮影しなければならないという制約のため,タイチン分子に外力を加えるとどのようにふるまうのかについてはよく分かっていなかった.そのため,様々な仮説が立てられた.
この疑問を説明しうる機序として,この ‘winding filament’ 仮説が有力視されてきた.
ざっくり説明すると,ポジティブ収縮の際にミオシンが発生する動力の大部分は収縮そのものに消費されるが,その一部が弾性ポテンシャルエナジーとしてタイチン分子内に蓄積され,ネガティブ収縮の際に放出されるのである.その蓄積の機序を最初に説明したのが ‘winding filament’ 仮説である.最初に「巻きつき」と書いたが,タイチンがアクチンに巻きついて弾性ポテンシャルエナジーを蓄積しているのではないか,そしてネガティブ収縮の際には巻きついたタイチンがほどけて蓄積したエネルギーを開放するためにポジティブ収縮よりも強い出力が得られるのではないか,というのが本論文の趣旨である.
しかし実はこの ‘winding filament’ 仮説は,最新の研究で否定されつつあるように見える.原子間力顕微鏡および磁気ピンセットによる研究ではタイチン分子の折りたたみが関わる,いわゆる titin folding 仮説 が優勢である.この分野はホットな領域であり,今後の研究が待たれる.
Is titin a ‘winding filament’? A new twist on muscle contraction Proc Biol Sci. 2012 Mar 7; 279(1730): 981–990.
要約
Recent studies have demonstrated a role for the elastic protein titin in active muscle, but the mechanisms by which titin plays this role remain to be elucidated. In active muscle, Ca2+-binding has been shown to increase titin stiffness, but the observed increase is too small to explain the increased stiffness of parallel elastic elements upon muscle activation. We propose a ‘winding filament’ mechanism for titin’s role in active muscle. First, we hypothesize that Ca2+-dependent binding of titin’s N2A region to thin filaments increases titin stiffness by preventing low-force straightening of proximal immunoglobulin domains that occurs during passive stretch. This mechanism explains the difference in length dependence of force between skeletal myofibrils and cardiac myocytes. Second, we hypothesize that cross-bridges serve not only as motors that pull thin filaments towards the M-line, but also as rotors that wind titin on the thin filaments, storing elastic potential energy in PEVK during force development and active stretch. Energy stored during force development can be recovered during active shortening. The winding filament hypothesis accounts for force enhancement during stretch and force depression during shortening, and provides testable predictions that will encourage new directions for research on mechanisms of muscle contraction.
キーワード
connectin, force enhancement, force depression, history dependence of force production, thin filament rotation, titin–actin interactions
最新の研究は,活動している筋肉における弾性蛋白タイチンの役割を明らかにしてきた.しかし,タイチンがこの役割をどのように演じるのかについては解明されていない.活動的な筋肉においては Ca2+ 結合がタイチンの硬度を増加させることが示されているが,観察された増加は小さすぎて筋肉活動上の並行弾性要素の硬度の増加を説明するには足りない.我々は活動する筋肉におけるタイチンの役割に ‘winding filament’ 機序を提案する.まず我々は仮定する, Ca2+ 依存性にタイチンの N2A 部位が細いフィラメントに結合することが,受動的ストレッチの間に起きる免疫グロブリン近位ドメインの弱い力のストレッチを阻害することによりタイチンの硬度を増加させる.この機序は,骨格筋原線維と心筋細胞の間の力の長さ依存性の違いを説明する.次に我々は仮定する,架橋はモーターとして細いフィラメントを M-line に引き寄せるだけでなく,タイチンをねじって細いフィラメントに巻きつけるローターとしても働き,筋出力増大とアクティブ短縮の間に PEVK において弾性ポテンシャルエナジーを蓄積するのであると.筋出力増大の間に蓄積されたエネルギーはアクティブ短縮の間に回復しうる.Winding filament 仮説はストレッチ中の力の増大と短縮中の力の抑制を説明し,筋収縮の機序の研究の新しい方向性を奨励する検証可能な指標を提供する.
導入
フィラメント滑走説 [1,2] の公開以降,筋収縮の分子メカニズム [3,4] の解明には著しい進展があった.この進展にもかかわらず,筋肉の機能のいくつかの問題に関する説明がまだ解明されておらず [5], それには伸展時に力が増強すること [6], 短縮時に筋力が低下すること [6],アクティブな伸展時の低コストな筋力産生 [7], 高い熱力学的効率での筋の活動的短縮 [8] が含まれる.これらおよびそれらの観察の結果,元の仮説の修正 [9] および別の仮説の発展 [10] につながった.
我々は揺動する架橋のフィラメント滑走説に新しい仮説を付け加えて提案する.筋サルコメアの二段階の ‘winding filament’ モデルは,その中でタイチンが Ca2+ 流入により活性化するのだが,その結果細いフィラメントが架橋により損傷し,細いフィラメントの翻転だけでなく回転も起こす.この仮説が,筋力の増強および減衰と同様に,筋生理学における他の未解明の観察をも理解する上で納得できる枠組みを提供することも示そう.
早期の構造研究 [2] から,タイチン様線維の存在が推測されていたにもかかわらず,コネクチンとしても知られるタイチンが発見されたのは,フィラメント滑走説が発展してから 20 年以上も後だった [11,12]. フィラメント滑走-架橋揺動説はタイチンを考慮せずに進展した.タイチンの早期の研究は,サルコメア集積の維持 [13] および横紋筋の受動的張力への寄与 [14] におけるその役割を確立した.現在の研究は筋原線維の集合の制御 [15] および細胞内シグナル [16] におけるタイチンの役割に焦点を当てている.その示唆するところによると,タイチンは休止期だけでなく活動時の筋肉においてもばねとして機能する可能性がある [17,18,19,20]. しかしながら,未だに,タイチンがいかにしてそのような役割を果たすのかについての説得力のある機序は提供されていない.
我々はまず,筋サルコメア内部のタイチンの配置について,筋肉の受動的張力へのタイチンの貢献について,さらに活動時の筋肉における力の産生へのタイチンの貢献について示した最新の研究をレビューする.続いて,我々は二段階の winding filament 仮説を発展させる.そこでは Ca2+ 流入がタイチンを「活性化」して Ca2+ 依存性に N2A が細いフィラメントに結合するのだが,タイチンのばねを短縮および硬化させ,架橋が細いフィラメントを翻転させるだけでなく回転させた後,タイチンはそれらに巻きつき,弾性ポテンシャルエナジーを PEVK 内に蓄積する.最後に,我々は筋肉のふるまいを理解するために winding filament 仮説の意義について議論しよう.
筋サルコメア内のタイチンの配置
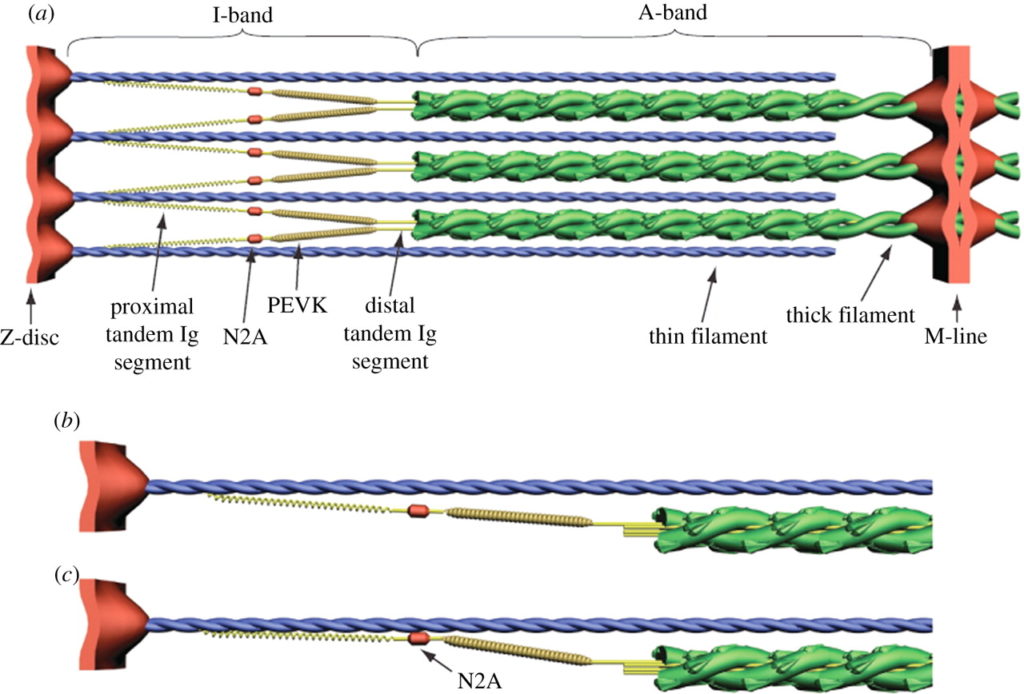
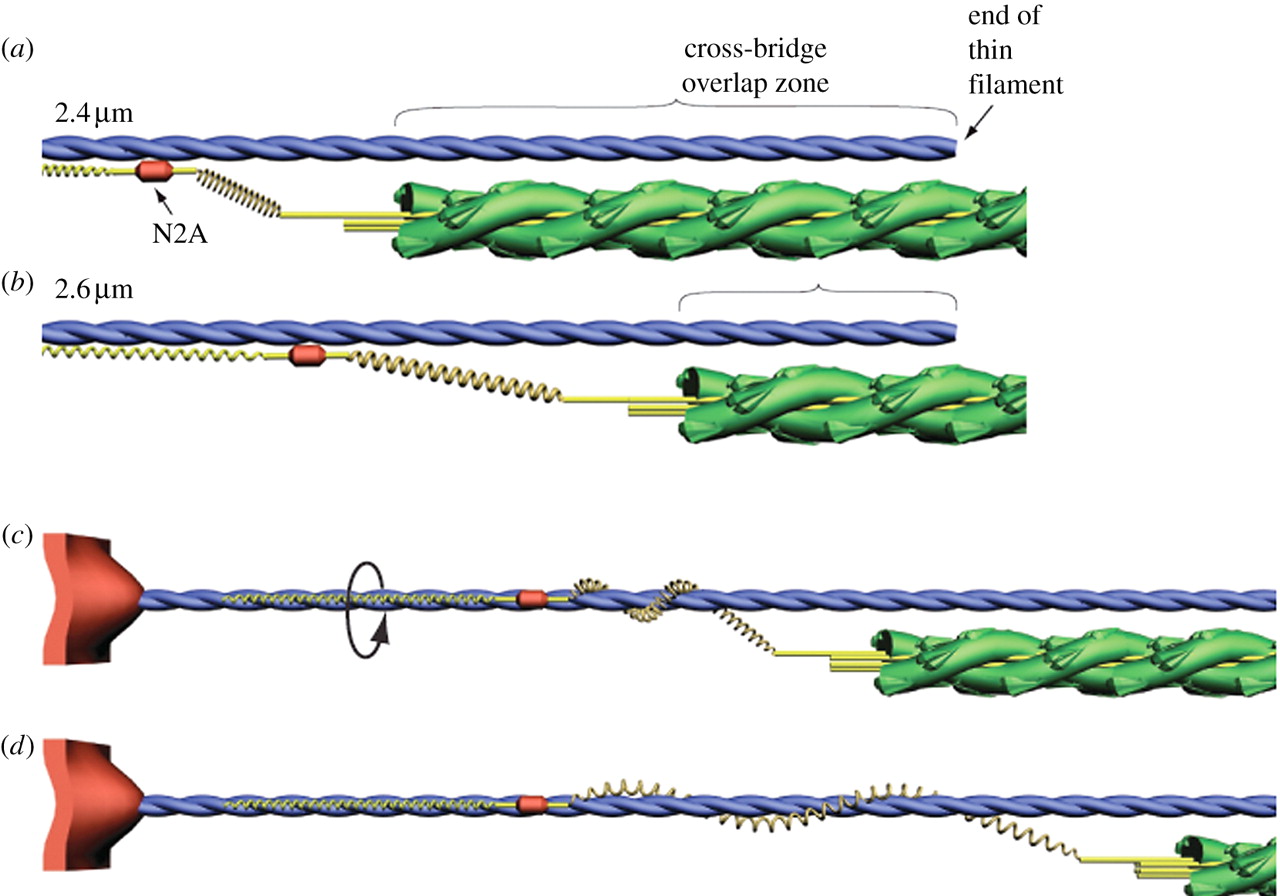
420 万ダルトンにも及ぶ,タイチンは既知の蛋白質の中で最大級であり [21], 横紋筋の中で 3 番目に豊富な蛋白質である [22]. タイチンは Z 盤から M-line まで,サルコメアの半分の長さにまたがる (1 µm) [15]. 各タイチン分子 (Figure 1a) は 1 本の太いフィラメントと A-band において結合し, 1 本の細いフィラメントと I-band において結合する [23]. 各サルコメアの半分において,各々の太いフィラメントは 6 本のタイチンフィラメントのコアを取り囲み,各々の細いフィラメントは 3 本のタイチンフィラメントと相互作用し,タイチンは隣接する太いフィラメントから放射状に伸びる [24]. 非伸張性のフィラメント末端は,6 本のタイチン分子の免疫グロブリン (Ig) 遠位ドメインから構成されるが, A/I 分岐部における各々の太いフィラメントの先端から出現する [24]. Ig ドメイン間の相互作用は,細いフィラメントの六角格子の中心におけるフィラメント末端の軸方向の位置を維持し,細いフィラメントは各々の太いフィラメントを取り囲む [24].
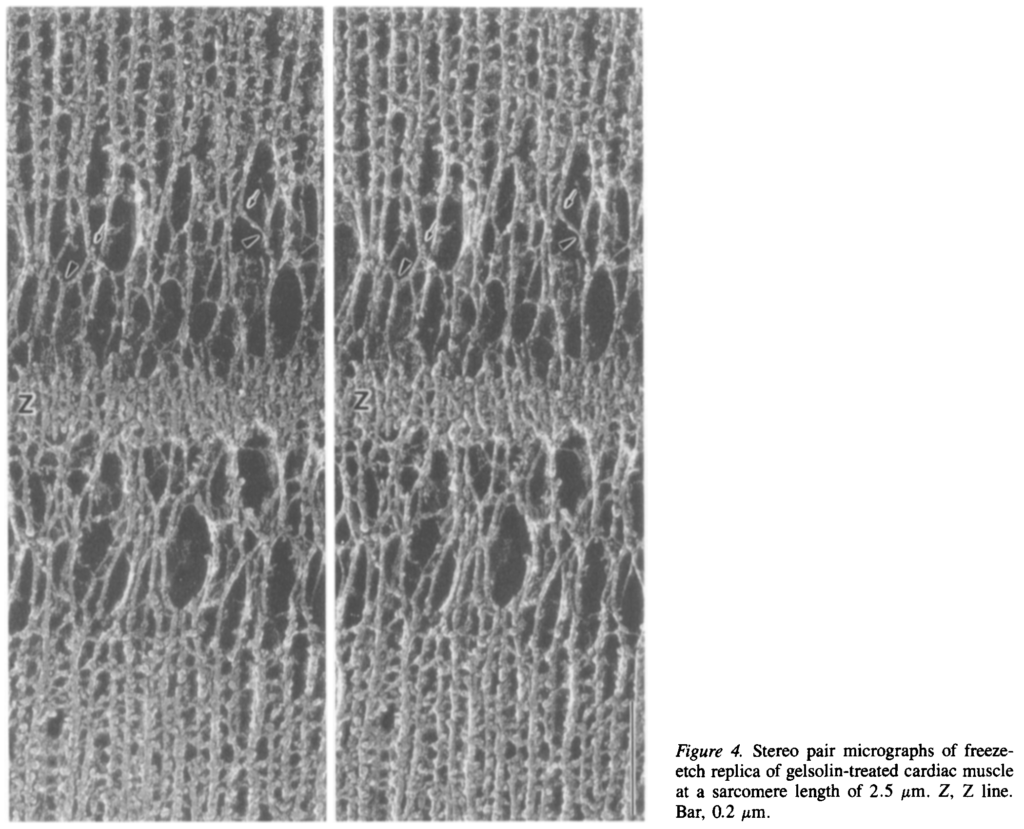
サルコメア長 2.5 µm における心筋細胞 Z line 近傍の電子顕微鏡による立体写真.上下に太いフィラメントがあり,中間に Z line がある.その間に弾性線維が見える.
タイチンのカルボキシ末端は M-line に位置し,そこではタイチンは逆の極性の重複でもって半サルコメアと隣接している [15]. A-band においては,タイチンはフィブロネクチン (FNIII) および Ig ドメインの繰り返しから構成され,太いフィラメントと強固に結合しているために伸長不能である [25]. I-band においては,タイチンは Ig セグメントの近位腕および遠位腕より構成され, PEVK 部位と隣接している.Ig 近位腕および PEVK セグメントは直列のばねとして機能する [14,26]. Z 盤においては,タイチンはサルコメアに隣接する細いフィラメント, α アクチニンおよび反平行タイチン分子に係留されている [27]. Z 盤および M-line 両者におけるタイチン分子の重複はタイチンフィラメントシステムを作り出し,それは全ての筋原線維の全長に渡るものである [15].
タイチンは筋肉の受動的張力に寄与する
多くの研究が無傷の筋原線維における受動的筋力と伸長の関連同様,個々のタイチン分子およびその部分について記述してきた [14,20,28]. サルコメア長が短いほど,折り畳まれた I-band タイチンの Ig ドメインを真っ直ぐにする受動的張力の増加は少ない [28,29]. サルコメア長が長いほど,PEVK ドメインが引き伸ばされ,受動的張力は急激に増加する [26,30]. PEVK は小さな力においては entropic spring としてふるまい,逆に強い力においては enthalpic spring または Hookean spring としてふるまう [14,31]. サルコメアが休止長 2.1-3.5 µm から伸展された際には, PEVK の長さは 10 倍以上に増加する [14]. 生理的なサルコメア長においては, PEVK の伸長が骨格筋原線維および心筋細胞の受動的弾性を大きく規定する [28,32]. 受動的張力が増加する局面では,サルコメア長は異なる筋肉で発現するタイチンのアイソフォームを変化させる [28].
活動中の筋肉においてタイチンの役割はあるのか?
活動中の筋線維において, Ca2+ 流入は非架橋構造,おそらくタイチンの張力と剛性を増加させる [19]. PEVK 断片と一個の筋線維の両者において, Labeit らは Ca2+ 流入がタイチンの剛性を増加させるだけでなく,筋原線維内の Ca2+ 増加が force-extension curve の左方偏位を起こすことを示した [20]. しかし,これらの試験で観察されたタイチン剛性での Ca2+ の効果は 10 倍程度であり,カルシウム活性化において筋線維の並行弾性剛性で観察される増加を考慮すると小さすぎる [19].
筋肉における力の増強はアクティブストレッチ後の定常状態の力の増加であり,対応する長さの等尺性の力を超え [6], それは受動的要素の動員による [33]. さらに,アクティブストレッチした筋線維の非アクティブ化後の受動的筋力は,受動的ストレッチ後や,対応する長さの等尺性収縮からの非アクティブ化後に産生される筋力より強く [18], さらには ‘passive force enhancement’ が受動的要素,いわゆるタイチンの動員によることが示唆された [18]. Joumaa らは筋原線維における受動的筋力増強を計測し,活動的筋力産生はトロポニン C の除去により阻害された [34]. Labeit らのように [20], 彼らもまた Ca2+ 誘発性のタイチンによる剛性の増加を観察したが,しかしその増加は受動的筋力増強を考慮すると小さすぎた.彼らの提案によると,受動的筋力増加は Ca2+ 流入だけでなく架橋形成や活動的筋力産生を要するというものである [34]. 太いフィラメントと細いフィラメントとの重なりを超えて(サルコメア長 > 3.8 µm)伸展された筋原線維において,Leonard と Herzog らは,タイチン剛性の活動依存性の増加および張力依存性の増加の両者のエビデンスを見出した [35]. これらのデータの示すところは,タイチン剛性は Ca2+ 流入および活動する筋肉における力の増加による,ということである.Winding filament 仮説は,以下で述べるが,活動するサルコメアでのタイチンによる張力への Ca2+ 流入および架橋サイクリングの影響の分子メカニズムを提供するものである.
Ca2+依存性のタイチンの細いフィラメントへの結合
N2A 部位 (Figure 1b, c) は Ca2+ 依存性に細いフィラメントに結合する間,タイチン剛性を修飾するにあたって理想的な位置にある.この部位でタイチンがアクチンに結合することは I-band における Ig ドメイン近位腕をまっすぐにする小さな力を制限する可能性があり, I-band は弛緩した長さの筋原線維の受動的ストレッチにより自然に発生する [14]. さらに, Ca2+ により活性化したサルコメアが伸展される時, PEVK セグメントは強い力で引き伸ばすことになる.仮に Ca2+ 依存性の N2A タイチンと細いフィラメント間の結合が阻害されれば, active force production は短いサルコメア長で減衰するはずである.タイチン内で発生したいかなる緊張も,強い力で PEVK セグメントを伸長するよりもむしろ小さな力で Ig セグメント椀を真っ直ぐにするはずである.ゆえに,タイチンの全ての active force に対するいかなる貢献も減少するだろう.
可能性のあるエビデンスの示唆するところでは,タイチンは Ca2+ 存在下に太いフィラメントに結合する.しかし,巨大なタイチン分子内部の結合部位の局在は分かっていない.骨格筋においては,タイチン分解産物 (T2) はアクチンに結合し, Ca2+ 依存性の方法で細いフィラメントを高い親和性に再構築する [36]. この T2 断片は約 200 万ダルトン,約 920 nm であり, C 末端, A-band FNIII, Ig ドメイン, PEVK および N2A 部位の一部を含む [37]. この N2A 部位にはエピトープがあり,それは p94/calpain3 と結合する [38]. この T2 断片は p94/calpain3 がタイチンを N2A 部位近傍の結合部位に消化する際に形成されると考えられている.Ca2+ 欠乏下では T2 と細いフィラメント間には弱い相互作用しか起きないが, Ca2+ が増加する (pCa = 4.5) と, T2 の細いフィラメントへの親和性が増加する [36]. 巨大な T2 断片内部の Ca2+ 依存性アクチン結合部位の局在はまだ同定されていない.
我々はこの Ca2+ 依存性アクチン結合部位がタイチンの N2A 内の T2 断片の N 末端に局在すると提案する (Figure 1b,c). 突然変異マウス (mdm) のヒラメ筋における我々の最近の研究が示唆するところでは,タイチンのエピトープは, N2A 領域の内部または近傍にあり, Ca2+ 存在下に細いフィラメントに結合するというものである [39]. マウスにおいては mdm 突然変異はタイチン遺伝子 N2A 領域の 779 塩基対の欠失を特徴とする [40]. 野生型マウスの筋肉において急速に免荷する間, force-displacement 曲線は休止状態の筋肉と比較して短い方向に活動をシフトさせる.休止状態に比べて活動期ではヒラメ筋でのタイチンばねは約 10 % 短縮し, 2.5 倍硬くなる.対照的に, mdm マウスからの活動する筋肉でのタイチンばねの長さと剛性の変化は観測されず, N2A 領域における多くのアミノ酸の欠損が起きている [39]. これらの観察から, Ca2+ 流入でのタイチン N2A の細いフィラメントへの結合がタイチンばねを短縮し剛性を増すという仮説が成り立つ.
Ca2+ 依存性の N2A–ACTIN 相互作用は長さ-張力関係に寄与する
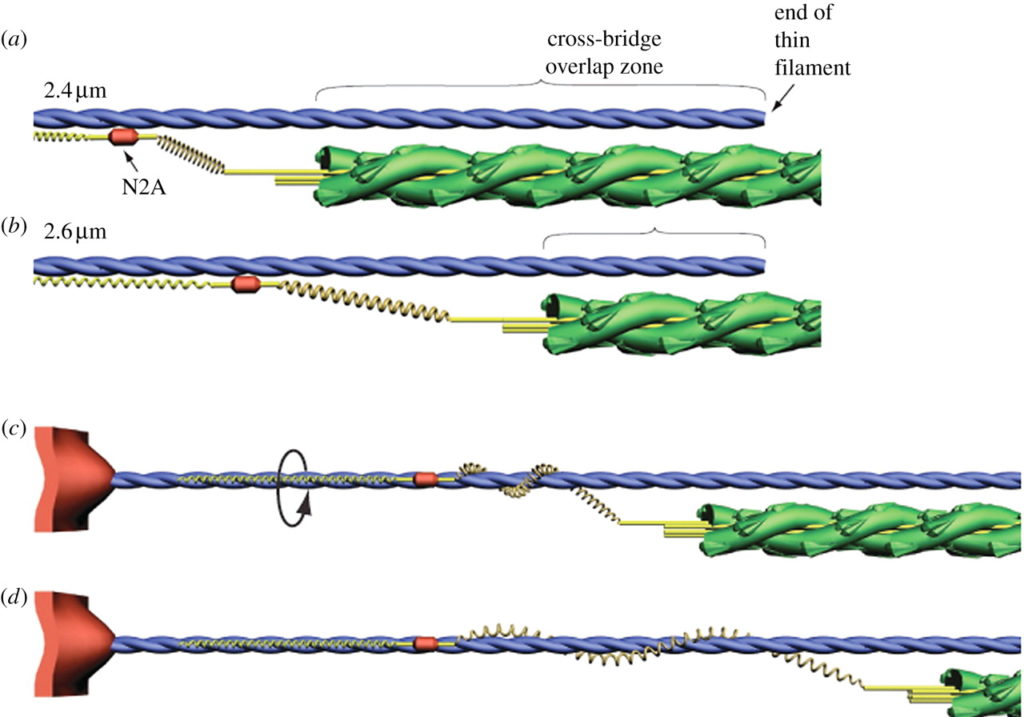
仮に N2A タイチンが細いフィラメント全長にわたって複数の結合部位を持つなら,筋肉の力と速度 [41] はサルコメア長が増加した時と相対的に同等だっただろう (Figure 2a,b). この方法では, Ca2+ 依存性 N2A タイチンの細いフィラメントへの結合はアクティブな長さ-張力関係におけるプラトーを強化し,それは太いフィラメントの中間にある自由領域の架橋に対応する [42].
筋生理学における未解決の疑問として,なぜ心筋には,骨格筋と対照的に,アクティブな長さ-張力関係におけるプラトーが存在しないのか,というものがある.そのプラトーは,細いフィラメント長の様々な基本から [43] 骨格筋におけるよりも心筋において最低でも広くまたはより幅広く存在するものと予想されている [42]. 骨格筋とは対照的に,タイチンの N2A アイソフォームが発現するところでは,マウスとラットの心室での心筋細胞は N2B アイソフォームのみを発現しており [44], Ca2+ 依存性のアクチンへの結合が存在しない [45]. それゆえ, mdm マウスからの筋肉のように,心筋細胞は N2A タイチンの細いフィラメントへの結合を欠いていると予想されている.ラットとマウスの心筋細胞は active force におけるプラトーを呈さない [46,47]. 対照的に,鱒からの心筋細胞はより巨大な N2AB アイソフォームを発現しており, N2A と N2B の両者を併せ持っているのだが,ゆえに Ca2+ 依存性の細いフィラメントへの結合を呈すると予想される.N2AB アイソフォームで提供された鱒心筋への追従の増加は拡張期におけるより大きな伸展を許すことになる.この仮説の予想するところは,鱒心筋細胞は,骨格筋のように,長さ-張力関係においてプラトーを呈するというものである [48].
心筋と骨格筋の重要な違いは,心筋はアクティブな時にも決して伸展されないことである.たとえ拡張期に受動的な長さを経ていたとしてもである [49]. ゆえに, Ca2+ 依存性のタイチンの剛性の増加は心筋では必要ない.対照的に,骨格筋は伸展の間は恒常的にアクティブであり [49,50,51], N2A というタイチンの一つのアイソフォームを持ち, Ca2+ 活性化での剛性が増加すると仮定される.
架橋サイクルは細いフィラメントを回転させるか?
活動時の筋サルコメアにおいて,架橋は細いフィラメントを翻転させるのと同様に回転させるだろう.太いフィラメントと細いフィラメントの構造が与えられると, Morgan は,アクチンモノマーと隣接する 3 本の太いフィラメント間の立体特異的な結合を維持するには,ミオシン頭部がアクチンモノマー一つ分の長さ (5.5 nm) を翻転する際に,細いフィラメントが約 28° 回転する必要があることを示した [10]. これは 71.5 nm の翻転ごとに細いフィラメントが 1 回転することを示している.
アクチンフィラメントのメロミオシン重鎖による回転は in vivo で観察されてきた [52,53,54]. Nishizaka らはミオシン頭部がアクチンフィラメントの長軸に対して右手系のトルクを生み出し,アクチン二重らせんに対して右回転のひねりを加えて巻き上げていることを観察した [53]. In vivo においては,アクチンとミオシン間の相互作用は筋サルコメアにおけるよりももっと拡散しており,アクチンフィラメントは 1 µm の翻転ごとに完全に一回転する [54].
筋サルコメアにおいては,アクチンフィラメントは Z 盤に係留されているため,架橋が細いフィラメントに対して回転だけでなくねじりを加えている可能性があり,アクチンらせんのヘリカルピッチの減少を生み出す [53]. X 線回折を用いると,細いフィラメントのヘリカルピッチにおける変化が活動時の筋線維において観察された [55,56]. 細いフィラメントもまた活動時には長さを変化させるという交絡因子が存在するにもかかわらず.Bordas らの観察によると,休止時と最大等尺運動時の間ではヘリカルピッチには差異は観察されなかった [55]. 細いフィラメントが最大等尺運動時に長くなったにもかかわらず.免荷状態の短縮ではアクチンフィラメントのヘリカルピッチは減少する.Tsaturyan らは細いフィラメントがさらに休止期より厳しくねじられていることを見出した [56]. 細いフィラメントで 1 µm の長さにわたり,緊密と休止間のヘリカルピッチにおいて観察された減少は,細いフィラメントの右手系の 270° のねじれに相当する.これらの観察から以下の仮説が成り立つ.すなわち,アクチンとの架橋相互作用は,力の発達と活動性短縮の間に,細いフィラメントの右手系の回転を生み出すと.
筋肉の活動時の Z 盤構造の変化もまた細いフィラメントの回転からなる. Z 盤においては,各々の細いフィラメントは 4 本の α アクチニン ‘lanyards’ により係留され,断面で見た時に休止期のサルコメアにおける小さな正方形パターンを形成する [57]. 筋肉が等尺性か等張性の力を発揮する時, Z 盤構造は小さな正方形から籠織りパターンに変化する [57]. α アクチニンの方向におけるこの変化は細いフィラメントの回転からなる [58].

WINDING FILAMENT 仮説
タイチンが太いフィラメントに A-band で結合し,細いフィラメントに Z 盤で結合しているため [23], 細いフィラメントの架橋による回転は,必然的にタイチンがそれらに巻き付く結果となる.タイチンフィラメントの架橋による回転はまた,Z 盤における α アクチニンへのトルクを作り出す可能性がある.タイチンの細いフィラメントへの巻きつきは長さの変化と PEVK の硬化を示唆しており,等尺性の力を発揮してアクティブに伸長する間,弾性ポテンシャルエナジーを蓄積するものである.このエネルギーはアクティブな収縮で回復する.
タイチンが細いフィラメントからの巻き付きをほどくことは PEVK と細いフィラメントの間の静電的相互作用により防がれる [31,45,59]. アクチンに結合した PEVK の自然解離速度は低く,その結合を破壊するにはアクチン-ミオシン架橋の破壊に匹敵するほどのエネルギーが必要である [59]. PEVK を細いフィラメントからほどくには次の前提が必要である.(i) 低強度での活動性収縮の間 [59], PEVK-アクチン結合体および架橋する力はあまりにも小さくてタイチンと α アクチニンとのトルクを保持できない. (ii) 筋弛緩の間も同様である.
タイチンは等尺性の力の発揮とアクティブストレッチの間に巻きつく
等尺性の力を発揮する間,我々が提案するのは,タイチンの細いフィラメントへの巻きつきは架橋する力の放射方向成分と,タイチンと α アクチニンとの放射方向成分の合計が釣り合うまで進行するというものである.力が増大するにつれて,細いフィラメントに巻き付いている PEVK 結合の長さは増加し, PEVK の自由部分における歪みまたは剛性,あるいはその両方を増加させる (Figure 2c). 活動するサルコメアが外力の働きにより伸ばされる時 (Figure 2d), 延長した自由 PEVK でなされた仕事は弾性ポテンシャルエナジーとして蓄積され,結果として低いエネルギーコストで力を増強できる可能性がある.
等尺性の力の増大およびアクティブストレッチの際の細いフィラメントの PEVK 上での回転の効果を定量化するため,我々は運動学モデルを作成した (Figure 3). そのモデルはサルコメア構造に基づき,ウサギ大腰筋に近似しており [14,60], 細いフィラメントの直径を 10 nm としており [61], タイチンフィラメントの直径を 4 nm としている [23,62]. SL = 2.6 µm での PEVK セグメントの長さはおよそ 104 nm である [14].
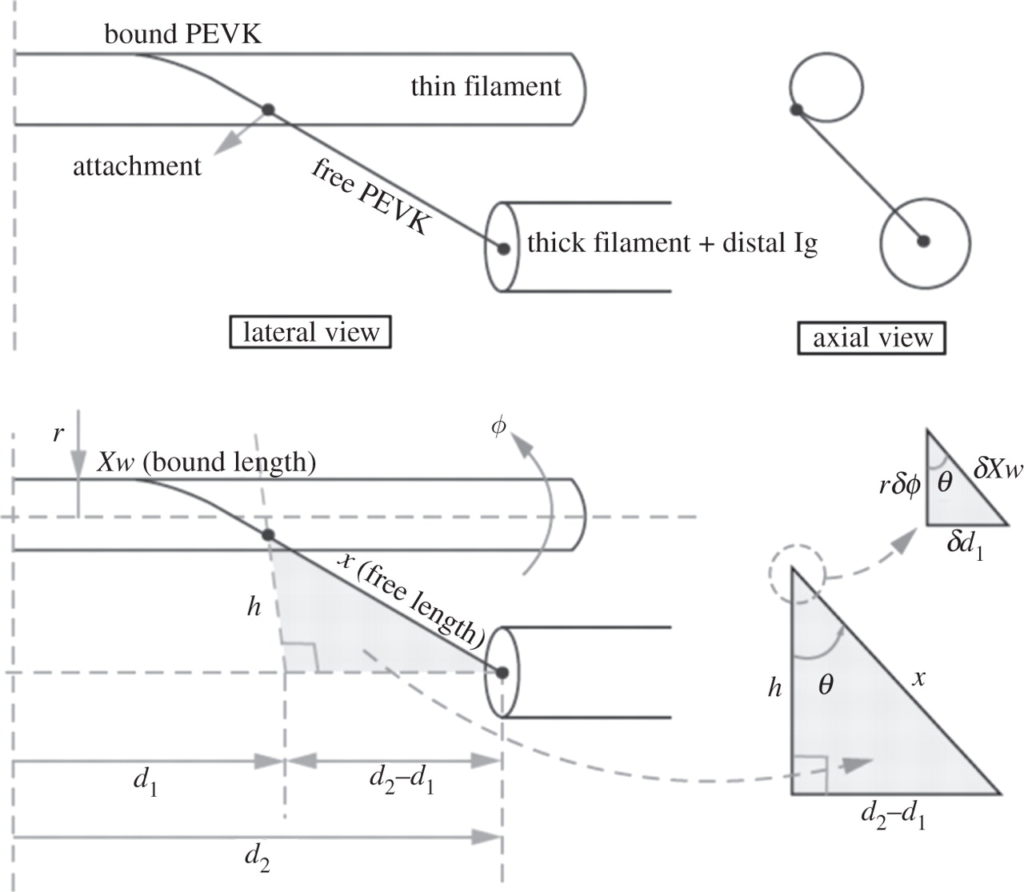
PEVK の歪みと剛性の増加は細いフィラメントの回転によるものであり,それは細いフィラメントへの巻き付き角度に依存する (Figure 3). 巻きつき角度 (θ) は細いフィラメントと PEVK が細いフィラメントに接触していない点で Z 盤に平行な線 (h) とのなす角度として定義される (Figure 3). そのモデルにおいては,巻きつき角度はサルコメアの幾何学的形状によってのみ定義され,ゆえにサルコメアの長さに伴って増加する.細いフィラメントの回転 (φ) が増加するにつれ,自由 PEVK セグメントの長さが減少することになり,ゆえにその効果的な剛性が増加する.しかし,自由末端と PEVK 結合末端の間の端は M-line に向かって伸びていき, PEVK の歪みを減少させる.そのモデルでは,タイチンは SL 2.4 µm の約 200° から SL 3.7 µm の約 30° まで様々に巻き付く.巻きつきの割合はアクチンのねじれ対回転により,アクチン対 α アクチニンの回転剛性に依存する.
PEVK 巻きつきの運動力学を近似するためにある線形常微分方程式が用いられ,その結果,細いフィラメントの回転 φ(t) およびサルコメアの幾何学的形状に関する所与のプロファイルに関する軸力が求まる.軸方向内では,力の総和は PEVK および架橋により産生される軸力の総和に等しい.軸平面内では, I-band 内の PEVK および Z 盤内の α アクチニンにより産生される放射方向の力によるトルクの総和は架橋力により産生されるトルクに等しく,反対方向である.架橋力は Pavlov らの報告に基づいて計算され [60], PEVK 力は Linke らの報告に基づいて計算され [14], α アクチニン内のトルクは指数関数的なばねとしてモデル化した.
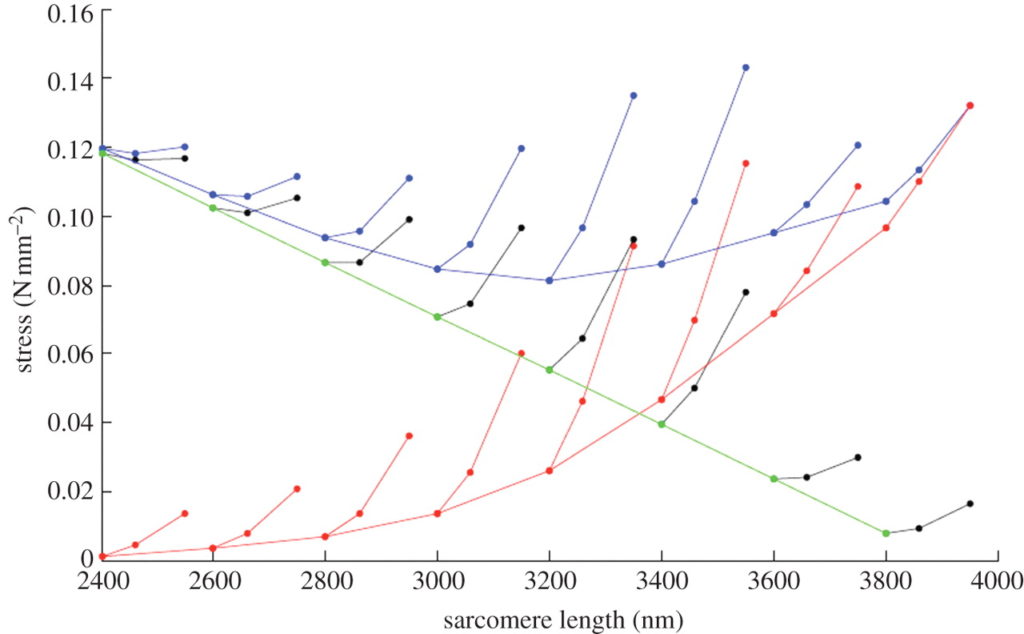
このモデルを用いて,我々は力-長さ関係の下肢筋力増強をシミュレーションし,異なる初期長で,ついで活動期にストレッチされる際に活性化されるサルコメア内の架橋およびタイチンにより産生される軸力を計算した (Figure 4). 結果は経験的な観察に定性的に近似していた [63]. これらの結果の示すところは, winding filament 仮説は,アクティブストレッチした筋肉に残った力の増強の観察されたパターンを考慮していることである.
アクティブ収縮期のタイチンの巻きつき
アクティブ短縮期においては架橋相互作用は細いフィラメントを M-line に向かって翻転させ, PEVK 内の弾性エネルギー蓄積を減少させるが,細いフィラメントを回転させ,エネルギー蓄積を増加させもする.架橋力に依存性により,収縮速度における責任因子およびステップサイズである PEVK は,架橋力が収縮速度を低下させるにつれて,ますます細いフィラメントからほどける.事実,そのような解けなしには,筋収縮の振幅は PEVK 結合により非現実的に制限されるだろう.
これらの考察の示唆するところは,アクティブ収縮期の総蓄積または弾性ポテンシャルエナジーの回復は,収縮速度に依存するということである.例えば,ある筋肉が最大等尺力に近い負荷に対してゆっくり収縮する時, 細いフィラメントの翻転による PEVK からの弾性エネルギーの回復は,細いフィラメントの回転による PEVK 内のエネルギー蓄積に比べて小さいだろう.さらには,高い架橋力と責任因子は PEVK が解けるのを阻害するだろう.ゆえに,その筋肉は収縮であるにもかかわらず PEVK 内の弾性エネルギーの総蓄積量を示すにとどまるだろう.
対照的に,小さな負荷に対して Vmax に近い速度で収縮する際には,架橋力と責任因子はより小さく,ステップサイズはより大きくなるだろう.というのは,細いフィラメント翻転による PEVK からの弾性エネルギー蓄積率は,細いフィラメント回転によるエネルギー蓄積率を上回るからである.さらに,架橋力が減少することで PEVK の解けを許すことになり,さらに弾性ポテンシャルエナジーの回復を増加させることになる.
同様に, winding filament モデルの示唆するところは, PEVK に蓄積された弾性エネルギーが散逸するほどの低負荷では,等張性収縮期の短縮速度が減少するだろうということである.短縮速度減少は負荷が小さいほど早くなるに違いない.というのは,蓄積した PEVK エネルギーは早い率で回復する可能性があるからである.このようにして, winding filament モデルは,等張性収縮期の負荷後の短縮率において観察された非線形性を考慮している [66].
Hill [66] らが最初に主張したのだが,活動する筋肉では短縮速度にあわせて短縮時の熱は単調増加する.彼の計測は後に改訂されたが,短縮熱は 0.5Vmax に達し,短縮速度の増加にもかかわらずその後は減少していった [67]. この関係の性質は Huxlay の二つの状態結合モデルによりよく示唆されていたにもかかわらず [68], そのモデルは収縮速度を 0.5Vmax より増やすのに必要なエネルギー源を特定していない.(このエネルギーが ATP 加水分解に由来するものでないことは銘記されたい.というのは,短縮熱が減衰するからである)この winding filament モデルは,弾性エネルギー蓄積から力学的エネルギーへの変換効率における増加に伴うところの ATPase における短縮速度の平準化とその後の減衰を説明する.
活動性サルコメアの即時弾力性
これは広く受け入れられていることだが,活動時の筋線維における即時弾力性は架橋内に単独で存在する [69]. 支持する根拠には以下の観察が含まれる.すなわち,一時的な力をゼロに(サルコメア半分あたり 4-14 nm [70])減少させるのに必要な長さの変化は一つの架橋ステップのオーダーに該当し,伸展した筋線維の弾力的ふるまいは,細いフィラメントと太いフィラメント間の重なりに直接比例して変化する [69].
しかしながら,活動するサルコメアの架橋単独で即時弾力性を説明できるのかについては反対意見も存在する [71]. 透過処理した単離筋線維の研究において,Galler と Hilber の報告では,一時的な力をゼロに減少させるのに必要な長さの変化は,温度を 6°C から 34°C に上げるとサルコメア半分あたり 6 から 18 nm に増加するという.彼らの結論は,より高い温度では, active force をゼロに減少させるのに必要な長さの変化は大きすぎて架橋の追従単独では説明できないとのことである.単離したカブトガニの telson の線維では,約 7 µm と極端に長いサルコメアを有しているのだが,力をゼロに減少させるのに必要な長さの変化はサルコメア半分あたり 270 nm である [73]. これに続いて Sugi らの示唆するところでは,タイチンが即時弾力性に寄与している可能性がある [73].
’Winding filament’ モデルの示唆するところは, PEVK の巻きつきによる緊張は活動する筋肉の即時弾力性に寄与している可能性があるというものだ.Winding filament モデルにおいては, PEVK の緊張は (i) 細いフィラメントの回転を非線形性に増加させ, (ii) 長さ-張力関係のプラトーが最大級であり, (iii) サルコメア長の増加を急速に減少させる.このモデルの示唆するところは, PEVK の緊張は,最適な長さで細いフィラメントの完全な回転には約 30 nm の率で蓄積する(ウサギ大腰筋で 2.4 µm).PEVK 緊張は下肢の長さ-張力関係ではさらにゆっくり蓄積する.
サルコメア長における不均一性は等尺性の力が発展する間に増大するが, quick release 時の一個の筋線維の即時弾力性に寄与している可能性がある [73]. 筋線維が等尺性に収縮する時,力の不均衡が隣接する半サルコメア内に生成し,その結果より弱いサルコメアがより強いサルコメアにより伸展され,その A-band はタイチンがその力と等しくなるまで伸展されて変位する.このようにして,タイチン分子は等尺性の力が発達する間即時弾力性に寄与し, quick release の際に観測される.
Sugi らはカブトガニ由来の単一の筋線維を研究した.カブトガニは珍しいことに 7 µm もの長さのサルコメアを有し,脊椎動物の筋肉に典型的な明確な M-line 構造を欠いている [73]. しかし,等尺性の力の発達する間に半サルコメアの不均一性が進展するのは,脊椎動物のサルコメアと同様の機能であることがわかった [60,74]. ウサギの大腰筋においては, A-band の約 60 nm の変位が最適な長さおよび最大の等尺性の力において観察される.観察される A-band の変位はまた即時弾力性に寄与すると推定されている.
過去十年間,単一の架橋が筋肉の独立した力の発生単位であるとの視点は修正されてきており,細いフィラメントと太いフィラメントの遵守に照らすと,全体として細いフィラメントと太いフィラメントの格子を含む [75]. Winding filament モデルにおいては,力の発生単位は弾力性のタイチンと α アクチニンフィラメントをも含む.というのは,架橋相互作用時に発生する放射方向の力を変換するからである.この視点は Shimamoto らの観察でも支持されており [76], 単一の筋原線維を α アクチニン抗体で処理するとサルコメア長が不均一の時同様,実質的に力の発生が阻害される.
WINDING FILAMENT モデルを解説する価値
Winding filament モデルはフィラメント滑走説を置き換えるものではない.代わりに,活動する筋サルコメア内部に弾性要素(タイチンなど)を加えて Ca2+ 流入と架橋サイクルにより修正し,winding filament モデルは,フィラメント滑走説単独では未解明のままだった現象を広範囲に安定して説明するものである.
History dependence
Active force production における歴史的変化はストレッチを伴う力の増強および短縮に伴う力の減衰を含む [6,63,77]. 活動性短縮後の筋肉により産生される定常状態の力は対応する長さの等尺性の力よりも小さく,同様に,活動性伸長後の定常状態の力は対応する長さの等尺性の力よりも高い.活動する筋肉のこれらの歴史依存的性質はばねに正確に期待されるものであり,その長さに応じて,伸展された時により大きな張力を産生し,短縮した時により小さな張力を産生する [78].
Winding filament モデルは短縮時の力の減衰も伸長時の力の増強もどちらの機序も提供する.活動短縮時に PEVK に蓄積されたエネルギーは力学的エネルギーに変換され,筋力は距離の短縮に直接比例して減少する.速度依存性に PEVK が細いフィラメントから解けることにより,力の減衰は短縮速度とともに増加する.短縮後には, PEVK が細いフィラメントに再度巻き付く架橋サイクルに伴い筋肉は力を回復する.アクティブストレッチの際には,伸展でなされた仕事は PEVK を引き伸ばし,弾性ひずみエネルギーを蓄積する.この付加的な力は距離の伸びとともに増加する.
フィラメント滑走説の示唆するところは,下肢の力-長さ曲線において active force の合計が,最適な重なりにおける最大等尺力を超過することは決してない,ということである.下肢の力-長さ曲線において筋伸展後の定常状態の active force は事実,最大等尺力を超過する可能性がある [18]. フィラメント滑走説と違い, winding filament 仮説は下肢の力-長さ曲線において active force が最大等尺力を上回る可能性を示唆している.
収縮を伸長することのコストの低さ
アクティブストレッチの際,筋肉はコンセントリック収縮時に産生されるのと同等の力ほど大きなエネルギーを要求しない [7]. あたかも活動する筋肉においてなされた何らかの仕事が,増強された力に吸収されるかのように見える.Winding filament モデルにおいては,外力がサルコメアを伸展する時に PEVK を伸展する際になされた仕事は弾性エネルギーとして蓄積され,筋力を増強させ,短縮時に解放される.
結論
タイチンの PEVK セグメントが筋力向上と活動性短縮に寄与することで,winding filament モデルは単純な機序を提供する.それは一般的な筋サルコメアの,特にタイチンの構造かつ粘弾性を構成する.それは揺動架橋-滑走フィラメント説の上に築かれ,説得力を増している.Winding filament モデルにおいては Ca2+ 依存性の N2A のタイチンフィラメントへの結合は I-band における Ig ドメイン近位腕の低力矯正を阻害し,それはたるんだ長さの骨格筋原線維に受動的張力を発生させる.このようにして力はプラトーに達し,骨格筋のサルコメア長の中間における強度に寄与する.
Winding filament モデルにおいて,架橋は細いフィラメントを ATP 加水分解の各周期に伴って回転させ,PEVK を細いフィラメントに巻きつける.この巻きつきは弾性エナジーを等尺性の力の発達の間 PEVK に蓄積する.蓄積したエネルギーは外部負荷依存性に短縮中に回復する.架橋の周期と PEVK 間の相互作用は弾性ポテンシャルエナジーの動力への変換効率を制御し,活動する筋肉に,負荷による摂動からの機械的安定性を付与する.活動性の伸長中,PEVK のなす外部仕事は筋力を増加させ,力の産生におけるエネルギーコストを減少させる.
Winding filament 仮説の決定的なテストは新しいナノスケールイメージングを待っており,それは 2 nm に近い直径の線維の動きを視覚化することができる.架橋がタイチンを細いフィラメントに巻きつけるという概念の直接的な証拠はないが,その概念を説明する価値には根拠がある.いくつか詳細については定量化されていないが,その仮説は検証可能な多くの予測を提供しており,筋収縮の機序における研究の新たな方向性を奨励するものである.
REFERENCES
1 Huxley, A. F. & Niedergerke, R. 1954 Structural changes in muscle during contraction. Nature 173, 971–973. (doi:10.1038/173971a0)
2 Huxley, H. & Hanson, J. 1954 Changes in the cross-striations of muscle during contraction and stretch and their structural interpretation. Nature 173, 973–976. (doi:10. 1038/173973a0)
3 Huxley, A. F. 2000 Mechanics and models of the myosin motor. Phil. Trans. R. Soc. Lond. B 355, 433–440. (doi:10.1098/rstb.2000.0584)
4 Huxley, H. E. 2000 Past, present and future experiments on muscle. Phil. Trans. R. Soc. Lond. B 355, 539–543. (doi:10.1098/rstb.2000.0595)
5 Herzog, W., Leonard, T. R., Joumaa, V. & Mehta, A. 2008 Mysteries of muscle contraction. J. Appl. Biomech. 24, 1–13.
6 Abbott, B. C. & Aubert, X. M. 1952 The force exerted by active striated muscle during and after change of length. J. Physiol. 117, 77–86.
7 Bigland-Ritchie, B. & Woods, J. J. 1976 Integrated electromyogram and oxygen uptake during positive and negative work. J. Physiol. (Lond.) 260, 267–277.
8 Kushmerick, M. J. & Davies, R. E. 1969 The chemical energetics of muscle contraction. II. The chemistry, efficiency and power of maximally working sartorius muscle. Proc. R. Soc. Lond. B 174, 315–353. (doi:10.1098/rspb. 1969.0096)
9 Julian, F. J. & Morgan, D. L. 1979 The effects of tension on non-uniform distribution of length changes applied to frog muscle fibres. J. Physiol. (Lond.) 293, 379–392.
10 Morgan, R. S. 1977 Actin rotates as myosin translates. J. Theor. Biol. 76, 769–771. (doi:10.1016/0022-5193 (77)90261-2)
11 Maruyama, K. 1976 Connectin, an elastic protein from myofibrils. J. Biochem. 80, 405–407.
12 Wang, K., McClure, J. & Tu, A. 1979 Titin: major myofibrillar components of striated muscle. Proc. Natl Acad. Sci. USA 76, 3698–3702. (doi:10.1073/pnas.76.8.3698)
13 Horowitz, R. & Podolsky, R. J. 1987 The positional stability of thick filaments in activated skeletal muscle depends on sarcomere length: evidence for the role of titin filaments. J. Cell Biol. 105, 2217–2223. (doi:10. 1083/jcb.105.5.2217)
14 Linke, W. A., Ivemeyer, M., Mundel, P., Stockmeier, M. R. & Kolmerer, B. 1998 Nature of PEVK–titin elasticity in skeletal muscle. Proc. Natl Acad. Sci. USA 95, 8052–8057. (doi:10.1073/pnas.95.14.8052)
15 Gregorio, C. C., Granzier, H., Sorimachi, H. & Labeit, S. 1999 Muscle assembly: a titanic achievement. Curr. Opin. Cell Biol. 11, 18–25. (doi:10.1016/S0955-0674 (99)80003-9)
16 Kru¨ger, M. & Linke, W. A. 2011 The giant protein titin: a regulatory node that integrates myocyte signalling pathways. J. Biol. Chem. 286, 9905–9912. (doi:10.1074/jbc. R110.173260)
17 Reich, T. E., Lindstedt, S. L., LaStayo, P. C. & Pierotti, D. J. 2000 Is the spring quality of muscle plastic? Am J. Physiol. 278, R1661–R1666.
18 Herzog, W. & Leonard, T. R. 2002 Force enhancement following stretching of skeletal muscle: a new mechanism. J. Exp. Biol. 205, 1275–1283.
19 Campbell, K. S. & Moss, R. L. 2002 History-dependent mechanical properties of permeabilized rat soleus muscle fibers. Biophys. J. 82, 929–943. (doi:10.1016/S0006- 3495(02)75454-4)
20 Labeit, D., Watanabe, K., Witt, C., Fujita, H., Wu, Y., Lahmers, S., Funck, T., Labeit, S. & Granzier, H. 2003 Calcium-dependent molecular spring elements in the giant protein titin. Proc. Natl Acad. Sci. USA 100, 13 716–13 721. (doi:10.1073/pnas.2235652100)
21 Warren, C. M., Krzesinski, P. R. & Greaser, M. L. 2003 Vertical agarose gel electrophoresis and electroblotting of high-molecular-weight proteins. Electrophoresis 24, 1695–1702. (doi:10.1002/elps.200305392)
22 Wang, K., Ramirez-Mitchell, R. & Palter, D. 1984 Titin is an extraordinarily long, flexible, and slender myofibrillar protein. Proc. Natl Acad. Sci. USA 81, 3685–3689. (doi:10.1073/pnas.81.12.3685)
23 Funatsu, T., Kono, E., Higuchi, H., Kimura, S., Ishiwata, S., Yoshioka, T., Maruyama, K. & Tsukita, S. 1993 Elastic filaments in situ in cardiac muscle: deepetch replica analysis in combination with selective removal of actin and myosin filaments. J. Cell Biol. 120, 711–724. (doi:10.1083/jcb.120.3.711)
24 Bennett, P. M., Hodkin, T. E. & Hawkins, C. 1997 Evidence that the tandem Ig domains near the end of the muscle thick filament form an inelastic part of the I-band titin. J. Struct. Biol. 120, 93–104. (doi:10.1006/ jsbi.1997.3898)
25 Muhle-Goll, C., Habeck, M., Cazorla, O., Nilges, M., Labeit, S. & Granzier, H. 2001 Structural and functional studies of titin’s fn3 modules reveal conserved surface patterns and binding to myosin S1: a possible role in the Frank–Starling mechanism of the heart. J. Mol. Biol. 313, 431–477. (doi:10.1006/jmbi.2001.5017)
26 Gautel, M. & Goulding, G. 1996 A molecular map of titin/connectin elasticity reveals two different mechanisms acting in series. FEBS Lett. 385, 11–14. (doi:10. 1016/0014-5793(96)00338-9)
27 Linke, W. A., Ivemeyer, M., Labeit, S., Hinssen, H., Ru¨egg, J. C. & Gautel, M. 1997 Actin–titin interaction in cardiac myofibrils: probing a physiological role. Biophys. J. 73, 905–919. (doi:10.1016/S0006-3495(97) 78123-2)
28 Wang, K., McCarter, R., Wright, J., Beverly, J. & Ramirez-Mitchell, R. 1991 Regulation of skeletal muscle stiffness and elasticity by titin isoforms: a test of the segmental extension model of resting tension. Proc. Natl Acad. Sci. USA 88, 7101–7105. (doi:10.1073/ pnas.88.16.7101)
29 Granzier, H. L. & Labeit, S. 2004 The giant protein titin: a major player in myocardial mechanics, signaling and disease. Circ. Res. 94, 284–295. (doi:10.1161/01.RES. 0000117769.88862.F8)
30 Trombitas, K., Greaser, M., French, G. & Granzier, H. 1998 PEVK extension of human soleus muscle titin revealed by immunolabeling with the anti-titin antibody 9D10. J. Struct. Biol. 122, 188–196. (doi:10.1006/jsbi. 1998.3984)
31 Linke, W. A., Kulke, M., Li, H., Fujita-Becker, S., Neagoe, C., Manstein, D. J., Gautel, M. & Fernandez, J. M. 2002 PEVK domain of titin: an entropic spring with actin binding properties. J. Struct. Biol. 137, 194–205. (doi:10.1006/ jsbi.2002.4468)
32 Magid, A. & Law, D. J. 1985 Myofibrils bear most of the resting tension in frog skeletal muscle. Science 230, 1280–1282. (doi:10.1126/science.4071053)
33 Edman, K. A. P. & Tsuchiya, T. 1996 Strain of passive elements during force enhancement by stretch in frog muscle fibres. J. Physiol. 490, 191–205.
34 Joumaa, V., Leonard, T. & Herzog, W. 2008 Residual force enhancement in myofibrils and sarcomeres. Proc. R. Soc. B 275, 1411–1419. (doi:10.1098/rspb. 2008.0142)
35 Leonard, T. R. & Herzog, W. 2010 Regulation of muscle force in the absence of actin–myosin based cross-bridge interaction. Am. J. Physiol. Cell Physiol. 299, 14–20. (doi:10.1152/ajpcell.00049.2010)
36 Kellermayer, M. S. Z. & Granzier, H. L. 1996 Calciumdependent inhibition of in vitro thin-filament motility by native titin. FEBS Lett. 380, 281–286. (doi:10.1016/ 0014-5793(96)00055-5)
37 Suzuki, J., Kimura, S. & Maruyama, K. 1994 Electron microscopic filament lengths of connectin and its fragments. J. Biochem. (Tokyo) 116, 406–410.
38 Hayashi, C. et al. 2008 Multiple molecular interactions implicate the connectin/titin N2A region as a modulating scaffold for p94/calpain 3 activity in skeletal muscle. J. Biol. Chem. 283, 14 801–14 814.
39 Monroy, J. A., Powers, K. L., Gilmore, L. A., Uyeno, T. A. & Nishikawa, K. C. 2011 Ca2+-activation of skeletal muscle: not just the thin filament? Integr. Comp. Biol. 51, e94. (doi:10.1093/icb/icr008)
40 Garvey, S. M., Rajan, C., Lerner, A. P., Frankel, W. N. & Cox, G. A. 2002 The muscular dystrophy with myositis (mdm) mouse mutation disrupts skeletal muscle-specific domain of titin. Genom 79, 146–149. (doi:10.1006/ geno.2002.6685)
41 Edman, K. A. P. 1979 The velocity of unloaded shortening and its relation to sarcomere length and isometric force in vertebrate muscle fibers. J. Physiol. 291, 143–159.
42 Allen, D. G. & Kentish, J. C. 1985 The cellular basis of the length–tension relation in cardiac muscle. J. Mol. Cell. Cardiol. 17, 821–840. (doi:10.1016/S0022-2828 (85)80097-3)
43 Robinson, T. F. & Winegrad, S. 1979 The measurement and dynamic implications of thin filament lengths in heart muscle. J. Physiol. 286, 607–619.
44 Cazorla, O., Freiburg, A., Helmes, M., Centner, T., McNabb, M., Wu, Y., Trombitas, K., Labeit, S. & Granzier, H. 2000 Differential expression of cardiac titin isoforms and modulation of cellular stiffness. Circ. Res. 86, 59–67.
45 Yamasaki, R. et al. 2001 Titin–actin interaction in mouse myocardium: passive tension modulation and its regulation by calcium/S100A1. Biophys. J. 81, 2297–2313. (doi:10.1016/S0006-3495(01)75876-6)
46 Weiwad, W. K. K., Linke, W. A. & Wussling, M. H. P. 2000 Sarcomere length–tension relationship of rat cardiac myocytes at lengths greater than optimum. J. Mol. Cell. Cardiol. 32, 247–259. (doi:10.1006/jmcc.1999.1069)
47 Shiels, H. A. & White, E. 2008 The Frank–Starling mechanism in vertebrate cardiac myocytes. J. Exp. Biol. 211, 2005–2013. (doi:10.1242/jeb.003145)
48 Patrick, S. M., Hoskins, A. C., Kentish, J. C., White, E., Shiels, H. A. & Cazorla, O. 2010 Enhanced lengthdependent Ca2+ activation in fish cardiomyocytes permits a large operating range of sarcomere lengths. J. Mol. Cell. Cardiol. 48, 917–924. (doi:10.1016/j. yjmcc.2010.02.008)
49 King, N. M., Mathawasin, M., Nedrud, J., Harrell, N., Chung, C. S., Helmes, M. & Granzier, H. 2010 Mouse intact cardiac myocyte mechanics: cross-bridge and titin-based stress in unactivated cells. J. Gen. Physiol. 137, 81–91. (doi:10.1085/jgp.201010499)
50 Biewener, A. & Roberts, T. J. 2000 Muscle and tendon contributions to force, work and elastic energy savings: a comparative perspective. Exerc. Sports Sci. Rev. 28, 99–107.
51 Dickinson, M. H., Farley, C. T., Full, R. J., Koehl, M. A. R., Kram, R. & Lehman, S. 2000 How animals move: an integrative view. Science 288, 100–106. (doi:10.1126/science.288.5463.100)
52 Tanaka, Y., Ishijima, A. & Ishiwata, S. 1992 Super helix formation of actin filaments in an in vitro motile system. Biochim. Biophys. Acta 159, 94–98. (doi:10.1016/0167- 4838(92)90079-S)
53 Nishizaka, T., Yagi, T., Tanaka, Y. & Ishiwata, S. 1993 Right-handed rotation of an actin filament in an in vitro motile system. Nature 361, 269–271. (doi:10.1038/ 361269a0)
54 Sase, I., Miyata, H., Ishiwata, S. & Kinosita, K. 1997 Axial rotation of sliding actin filaments revealed by single-fluorophore imaging. Proc. Natl Acad. Sci. USA 94, 5646–5650. (doi:10.1073/pnas.94.11.5646)
55 Bordas, J., Svensson, A., Rothery, M., Lowy, J., Diakun, G. P. & Boesecke, P. 1999 Extensibility and symmetry of actin filaments in contracting muscles. Biophys. J. 77, 3197–3207. (doi:10.1016/S0006-3495(99)77150-X)
56 Tsaturyan, A. K., Koubassova, N., Ferenczi, M. A., Narayanan, T., Roessle, M. & Bershitsky, S. Y. 2005 Strong binding of myosin heads stretches and twists the actin helix. Biophys. J. 88, 1902–1910. (doi:10. 1529/biophysj.104.050047)
57 Goldstein, M. A., Schroeter, J. P. & Sass, R. L. 1990 Two structural states of the vertebrate Z band. Electron Microsc. Rev. 3, 227–248. (doi:10.1016/0892-0354(90) 90003-B)
58 Jarosch, R. 2000 Muscle force arises by actin filament rotation and torque in the Z-filaments. Biochem. Biophys. Res. Commun. 270, 677–682. (doi:10.1006/bbrc.1999.1971)
59 Bianco, P., Nagy, A., Kengyel, A., Szatmari, D., Martonfalvi, Z., Huber, T. & Kellermayer, M. S. Z. 2007 Interaction forces between F-actin and titin PEVK domain measured with optical tweezers. Biophys. J. 93, 2102–2109. (doi:10.1529/biophysj.107.106153)
60 Pavlov, I., Novinger, R. & Rassier, D. 2009 The mechanical behavior of individual sarcomeres of myofibrils isolated from rabbit psoas muscle. Am. J. Physiol. Cell Physiol 297, C1211–C1219. (doi:10.1152/ajpcell.00233.2009)
61 Shi, D., Somlyo, A. V., Somlyo, A. P. & Shao, Z. 2001 Visualizing filamentous actin on lipid bilayers by atomic force microscopy in solution. J. Microsc. 201, 377–382. (doi:10.1046/j.1365-2818.2001.00844.x)
62 Higuchi, H., Nakauchi, Y., Maruyama, K. & Fujime, S. 1993 Characterization of beta-connectin (titin 2) from striated muscle by dynamic light scattering. Biophys. J. 65, 1906–1915. (doi:10.1016/S0006-3495 (93)81261-X)
63 Edman, K. A. P., Elzinga, G. & Noble, M. I. M. 1982 Residual force enhancement after stretch of contracting frog single muscle fibers. J. Gen. Physiol. 80, 769–784. (doi:10.1085/jgp.80.5.769)
64 Finer, J. T., Mehta, A. D. & Spudich, J. A. 1995 Characterization of single actin–myosin interactions. Biophys. J. 68, S291–S296. (doi:10.1016/S0006-3495 (95)80187-6)
65 Reconditi, M. et al. 2004 The myosin motor in muscle generates a smaller and slower working stroke at higher load. Nature 428, 578–581. (doi:10.1038/nature02380)
66 Hill, A. V. 1938 The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. B 126, 136–195. (doi:10.1098/rspb.1938.0050)
67 Hill, A. V. 1964 The effect of load on the heat of shortening of muscle. Proc. R. Soc. Lond. B 159, 297–318. (doi:10.1098/rspb.1964.0004)
68 Huxley, A. F. 1973 A note suggesting that the crossbridge attachment during muscle contraction may take place in two stages. Proc. R. Soc. Lond. B 183, 83–86. (doi:10.1098/rspb.1973.0006)
69 Huxley, A. F. & Simmons, R. M. 1971 Proposed mechanism of force generation in striated muscle. Nature 233, 533–538. (doi:10.1038/233533a0)
70 Ford, L. E., Huxley, A. F. & Simmons, R. M. 1977 Tension responses to sudden length change in stimulated frog muscle fibers near slack length. J. Physiol. 269, 441–515.
71 Lappin, A. K., Monroy, J. A., Pilarski, J. Q., Zepnewski, E. D., Pierotti, D. J. & Nishikawa, K. C. 2006 Storage and recovery of elastic potential energy powers ballistic prey capture in toads. J. Exp. Biol. 209, 2535–2553. (doi:10.1242/jeb.02276)
72 Galler, S. & Hilber, K. 1998 Tension/stiffness ratio of skinned rat skeletal muscle fibre types at various temperatures. Acta Physiol. Scand. 162, 119–126. (doi:10.1046/j. 1365-201X.1998.0272f.x)
73 Sugi, H., Akimoto, T., Kobayashi, T., Suzuki, S. & Shimada, S. 2000 Possible contribution of titin filaments to the compliant series elastic component in horseshoe crab skeletal muscle fibers. Adv. Exp. Med. Biol. 481, 371–380. (doi:10.1007/978-1-4615-4267-4_22)
74 Telley, I. A., Stehle, R., Ranatunga, K. W., Pfitzer, G., Stu¨ssi, E. & Denoth, J. 2006 Dynamic behaviour of half-sarcomeres during and after stretch in activated rabbit psoas myofibrils: sarcomere asymmetry but no ‘sarcomere popping’. J. Physiol. 573, 173–185. (doi:10. 1113/jphysiol.2006.105809)
75 Daniel, T. L., Trimble, A. C. & Chase, P. B. 1998 Compliant realignment of binding sites in muscle: transient behavior and mechanical tuning. Biophys. J. 74, 1611–1621. (doi:10.1016/S0006-3495(98)77875-0)
76 Shimamoto, Y., Suzuki, M., Mikhailenko, S. V., Yasuda, K. & Ishiwata, S. 2009 Inter-sarcomere coordination in muscle revealed though individual sarcomere response to quick stretch. Proc. Natl Acad. Sci. USA 106, 11 954–11 959. (doi:10.1073/pnas.0813288106)
77 Edman, K. A. 1975 Mechanical deactivation induced by active shortening in isolated muscle fibers of the frog. J. Physiol. 246, 255–275. 78 Monroy, J. A., Lappin, A. K. & Nishikawa, K. C. 2007 Elastic properties of active muscle: on the rebound? Exerc. Sports Sci. Rev. 35, 174–179. (doi:10.1097/jes. 0b013e318156e0e6)
78 Monroy, J. A., Lappin, A. K. & Nishikawa, K. C. 2007 Elastic properties of active muscle: on the rebound? Exerc. Sports Sci. Rev. 35, 174–179. (doi:10.1097/jes. 0b013e318156e0e6)


“タイチンは’winding filament’なのか?筋収縮における新たなねじれ” への2件の返信