人体には暑熱馴化という機構がある.暑さに体が慣れることである.この機構を取り込んだモデルを構築してみた.
暑熱馴化とは
暑さに体を徐々に慣らしていくことを言う.暑熱順化とも書く.暑熱馴化が充分でないとより低温でも熱中症が起きやすいとされる.夏の気候が進むに連れて暑熱馴化した個体が増えていくと予想される.
暑熱馴化をモデルに取り込むには
おそらく時間経過の変数を取り込むのが良いだろうと検討をつけた.具体的には月である.『気象データから熱中症救急搬送者数を予測する』という日本救急医学会の原著論文では7月と8月で暑熱馴化を分けていたため,年月日を7月末日までと8月1日以降で分けるモデルを構築してみた.一方,夏の気候が進むにつれて暑熱馴化した個体が増えると予想されることから,月をそのまま変数として投入するモデルも必要と考えられた.
クエリ
下記クエリをSQL Serverで発行して結果をEXCELにコピペしHeatStroke4.xlsxという名前で保存する.
USE HeatStrokeDB; GO SELECT P.FiscalYear , T.年月日 AS Date , MONTH(T.年月日) AS Month , CASE WHEN MONTH(T.年月日)<= 7 THEN 1 ELSE 0 END AS Acclimation , T.都道府県コード AS PrefCode , T.都道府県 AS Pref , T.日最高気温 AS Temp , V.日平均蒸気圧 AS Vapor , W.平均風速 AS Wind , C.平均雲量 AS Cloud , P.Population AS Pop , H.[搬送人員(計)] AS Num FROM dbo.T_HeatStroke AS H INNER JOIN dbo.T_MaxTemperature AS T ON H.都道府県コード = T.都道府県コード AND H.日付 = T.年月日 INNER JOIN dbo.T_VaporPressure AS V ON H.都道府県コード = V.都道府県コード AND H.日付 = V.年月日 INNER JOIN dbo.T_Wind AS W ON H.都道府県コード = W.都道府県コード AND H.日付 = W.年月日 INNER JOIN dbo.T_Population AS P ON H.都道府県コード = P.PrefCode AND YEAR(H.日付) = P.FiscalYear INNER JOIN dbo.T_Cloud AS C ON H.都道府県コード = C.都道府県コード AND H.日付 = C.年月日 ORDER BY PrefCode, Date
(63725 行処理されました)
Rでの処理
下記コードを実行する.
> y = HeatStroke4$Num > x1 = HeatStroke4$Temp > x2 = HeatStroke4$Vapor > x5 = HeatStroke4$Acclimation > x6 = HeatStroke4$Month > p = HeatStroke4$Pop > z1 = glm(y ~ x1 + x2, offset = log(p), family = poisson(link = "log")) > z2 = glm(y ~ x1 + x2 + x5, offset = log(p), family = poisson(link = "log")) > z3 = glm(y ~ x1 + x2 + x6, offset = log(p), family = poisson(link = "log"))
結果は次のとおりである.7月と8月で分けた場合,7月以前の係数の符号は正であり,同じ最高気温,同じ平均水蒸気圧でも,8月以降よりも搬送人員数は多くなることが予想される.月を変数として投入した場合,係数の符号は負であり,月が進むほど同じ最高気温,平均水蒸気圧でも搬送人員数が少なくなると予想される.
また7月と8月で分けるよりも,月を変数としてそのまま投入したほうがAICは良い.モデルの予測性能としては月をそのまま投入したほうが良さそうである.
> summary(z1)
Call:
glm(formula = y ~ x1 + x2, family = poisson(link = "log"), offset = log(p))
Deviance Residuals:
Min 1Q Median 3Q Max
-12.8521 -1.2624 -0.4054 0.9833 19.8305
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.288e+01 1.682e-02 -1360.2 <2e-16 ***
x1 2.735e-01 5.367e-04 509.6 <2e-16 ***
x2 6.379e-02 4.275e-04 149.2 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 857600 on 63724 degrees of freedom
Residual deviance: 264558 on 63722 degrees of freedom
AIC: 428808
Number of Fisher Scoring iterations: 5
> summary(z2)
Call:
glm(formula = y ~ x1 + x2 + x5, family = poisson(link = "log"),
offset = log(p))
Deviance Residuals:
Min 1Q Median 3Q Max
-12.2137 -1.1973 -0.3776 0.9475 21.2504
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.352e+01 1.741e-02 -1350.8 <2e-16 ***
x1 2.823e-01 5.402e-04 522.6 <2e-16 ***
x2 6.884e-02 4.273e-04 161.1 <2e-16 ***
x5 4.482e-01 2.883e-03 155.5 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 857600 on 63724 degrees of freedom
Residual deviance: 240471 on 63721 degrees of freedom
AIC: 404723
Number of Fisher Scoring iterations: 5
> summary(z3)
Call:
glm(formula = y ~ x1 + x2 + x6, family = poisson(link = "log"),
offset = log(p))
Deviance Residuals:
Min 1Q Median 3Q Max
-11.9928 -1.1828 -0.3778 0.9220 20.9818
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.136e+01 1.820e-02 -1173.8 <2e-16 ***
x1 2.843e-01 5.423e-04 524.3 <2e-16 ***
x2 7.738e-02 4.274e-04 181.1 <2e-16 ***
x6 -2.985e-01 1.776e-03 -168.1 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 857600 on 63724 degrees of freedom
Residual deviance: 235494 on 63721 degrees of freedom
AIC: 399746
Number of Fisher Scoring iterations: 5
ロジスティック関数の導入
更に考察を進める.月をモデルに投入する際,1次の線形で投入したが,暑熱馴化した個体数は時間経過とともにシグモイド曲線を描くと考えられる.7月では暑熱馴化した個体数はまだ少なく,9月では馴化した個体数は十分に増加していると考えられ,8月はまさに馴化の最中であると考えられる.実際,8月上旬が最も暑い.そのような曲線を描くのに適した関数がロジスティック関数である.
ここからは試行錯誤になる.
上記のグラフを描いてみると6月から9月にかけての傾きは線形の場合とほぼ変わらない.
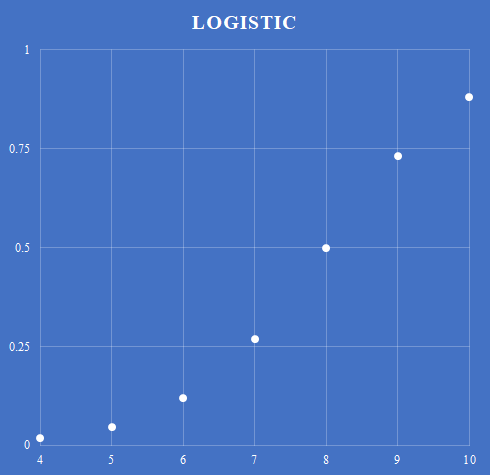
そこで線形予測子の項に2をかけてみる.
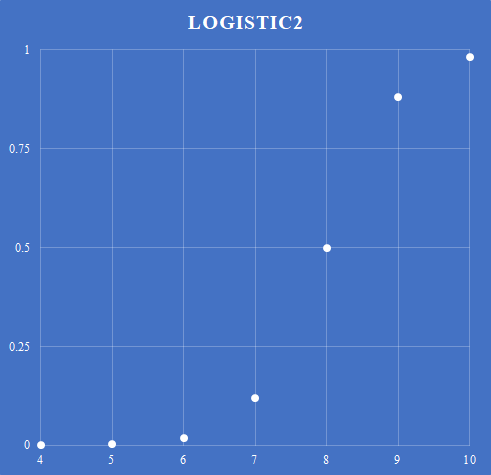
このグラフだと7月は比較的少なく,8月に急峻に立ち上がり,9月には多く安定するという曲線が得られる.この関数を使用してみる.
> y = HeatStroke7$Num > x1 = HeatStroke7$Temp > x2 = HeatStroke7$Vapor > x3 = HeatStroke7$Month > x4 = exp(HeatStroke7$Month) > x5 = 1/(1 + exp(8 - HeatStroke7$Month)) > x6 = 1/(1 + exp(16 - 2 * HeatStroke7$Month)) > p = HeatStroke7$Pop > z3 = glm(y ~ x1 + x2 + x3, offset = log(p), family = poisson(link = "log")) > z4 = glm(y ~ x1 + x2 + x4, offset = log(p), family = poisson(link = "log")) > z5 = glm(y ~ x1 + x2 + x5, offset = log(p), family = poisson(link = "log")) > z6 = glm(y ~ x1 + x2 + x6, offset = log(p), family = poisson(link = "log"))
> summary(z3)
Call:
glm(formula = y ~ x1 + x2 + x3, family = poisson(link = "log"),
offset = log(p))
Deviance Residuals:
Min 1Q Median 3Q Max
-12.1367 -1.2075 -0.3934 0.9025 20.9325
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.140e+01 1.694e-02 -1263.8 <2e-16 ***
x1 2.841e-01 5.083e-04 559.0 <2e-16 ***
x2 8.104e-02 3.997e-04 202.8 <2e-16 ***
x3 -3.026e-01 1.664e-03 -181.8 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 984714 on 70107 degrees of freedom
Residual deviance: 263517 on 70104 degrees of freedom
AIC: 446465
Number of Fisher Scoring iterations: 5
> summary(z4)
Call:
glm(formula = y ~ x1 + x2 + x4, family = poisson(link = "log"),
offset = log(p))
Deviance Residuals:
Min 1Q Median 3Q Max
-12.5525 -1.1976 -0.3893 0.9082 21.1380
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.255e+01 1.553e-02 -1452.0 <2e-16 ***
x1 2.706e-01 5.000e-04 541.2 <2e-16 ***
x2 6.747e-02 3.938e-04 171.3 <2e-16 ***
x4 -1.274e-04 7.212e-07 -176.6 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 984714 on 70107 degrees of freedom
Residual deviance: 261180 on 70104 degrees of freedom
AIC: 444128
Number of Fisher Scoring iterations: 5
> summary(z5)
Call:
glm(formula = y ~ x1 + x2 + x5, family = poisson(link = "log"),
offset = log(p))
Deviance Residuals:
Min 1Q Median 3Q Max
-12.0329 -1.2065 -0.3907 0.9017 20.8520
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.286e+01 1.554e-02 -1470.9 <2e-16 ***
x1 2.812e-01 5.052e-04 556.6 <2e-16 ***
x2 7.606e-02 3.965e-04 191.8 <2e-16 ***
x5 -1.485e+00 8.081e-03 -183.7 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 984714 on 70107 degrees of freedom
Residual deviance: 262084 on 70104 degrees of freedom
AIC: 445032
Number of Fisher Scoring iterations: 5
> summary(z6)
Call:
glm(formula = y ~ x1 + x2 + x6, family = poisson(link = "log"),
offset = log(p))
Deviance Residuals:
Min 1Q Median 3Q Max
-12.2273 -1.2029 -0.3876 0.9039 20.7392
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.286e+01 1.561e-02 -1464.9 <2e-16 ***
x1 2.777e-01 5.029e-04 552.2 <2e-16 ***
x2 7.139e-02 3.958e-04 180.4 <2e-16 ***
x6 -9.866e-01 5.305e-03 -186.0 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 984714 on 70107 degrees of freedom
Residual deviance: 260900 on 70104 degrees of freedom
AIC: 443848
Number of Fisher Scoring iterations: 5
最後のモデルz6でAICが最も小さくなった.
まとめ
暑熱順応を考慮したモデルを構築した.
暑熱馴化を表現するためにロジスティック関数を導入したが,本来ならば1年を周期とした三角関数を用いるべきであろう.
余談だが,先に引用した論文では平均気温から予測式を導出し,その形が指数関数であることからポアソン分布を想定していると考えられる.しかし暑熱馴化の補正項を指数関数の外に出している.筆者は統計学初心者でありこのような補正が適切なのか,指数関数内の線形予測子で対応すべきなのかは判断できない.東京,大阪,神奈川の3都府県はよく一致しているが,他の道府県では一致の程度がどうなのか論文では紹介されておらず,気になる.論文著者に聞いてみたいところである.
