ポアソン回帰モデルおよび負の二項分布モデルを用いて熱中症搬送人員数に対する日最高気温と平均水蒸気圧の回帰係数を推定する

　以前，熱中症搬送人員数は日最高気温と相関関係があり，片対数グラフで直線になると述べた．今回はポアソン回帰モデルおよび負の二項分布モデルで熱中症搬送人員数に対する日最高気温と平均水蒸気圧の回帰係数を推定する．

SQL Serverからデータを抽出する

　下記クエリを実行してデータベースHeatStrokeDBからデータを抽出し，結果をExcelにコピペして保存する．ファイル名をHeatStroke.xlsxとする．

USE HeatStrokeDB;
GO
SELECT	H.日付	AS Date
	,	H.都道府県コード	AS PrefCode
	,	M.都道府県	AS Pref
	,	M.日最高気温	AS Temp
	,	V.日平均蒸気圧	AS Vapor
	,	H.[搬送人員（計）]	AS HeatStroke
FROM	dbo.T_HeatStroke	AS H
INNER	JOIN	dbo.T_MaxTemperature	AS M
ON	H.都道府県コード=M.都道府県コード
AND	H.日付=M.年月日
INNER	JOIN	dbo.T_VaporPressure	AS V
ON	H.都道府県コード=V.都道府県コード
AND	H.日付=V.年月日
ORDER	BY	PrefCode, Date

ExcelのファイルをRで読み込む

　EnvironmentタブのImport Datasetを押下しFrom Excel…を選択する．

　ユーザーインターフェースでダイアログが開くので，先程保存した目的のファイルを開く．

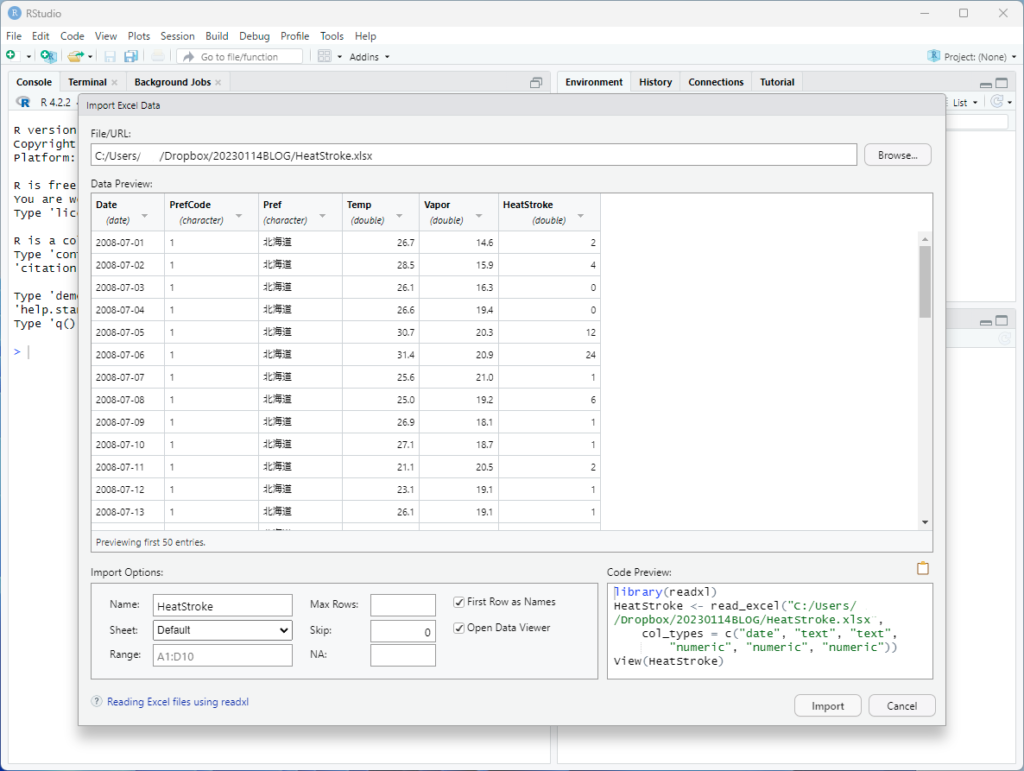
　データ型の変更ができる．Date列を日付型に変更し，PrefCode列を文字列型に変更し，Importをクリックする．

　HeatStrokeという変数にExcelのデータが格納された状態．この変数はデータフレームと呼ばれ，ここからデータを取り出していく．

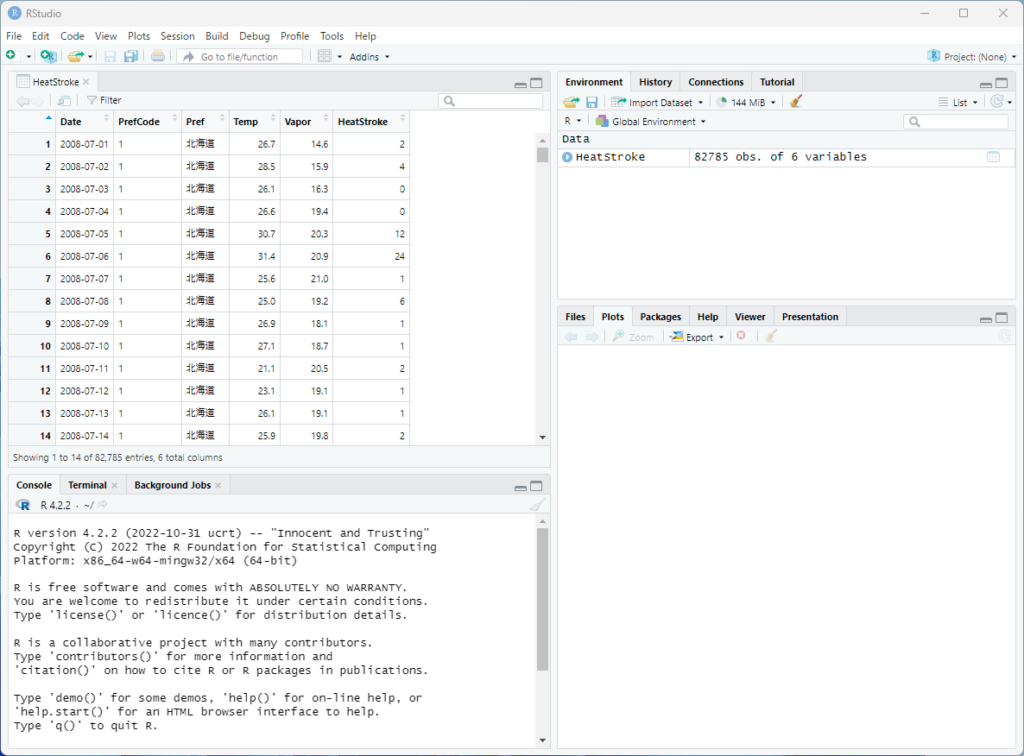
Rでの操作

　コンソールはデフォルトでは左下にある．データフレームから各列のデータを取り出すにはデータフレーム名$列名と記述する．

各列の抽出

　下記のように最高気温をvTemp，平均水蒸気圧をvVapor，搬送人員数をvNumと決め，それぞれ抽出する．コード補完が働き，変数名を補完してくれる．

> vTemp=HeatStroke$Temp
> vVapor=HeatStroke$Vapor
> vNum=HeatStroke$HeatStroke

散布図の描画

　下記のように記述する．

> plot(vTemp, vNum)
> plot(vVapor, vNum)

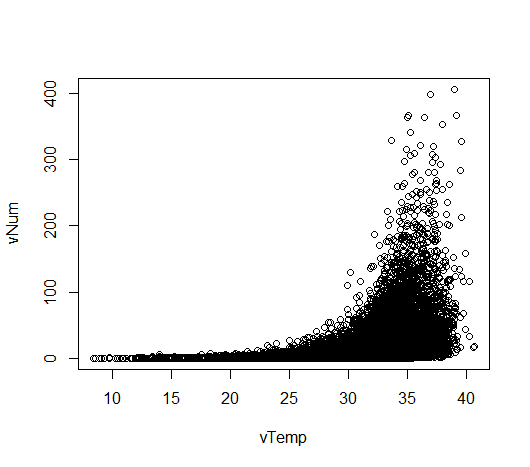
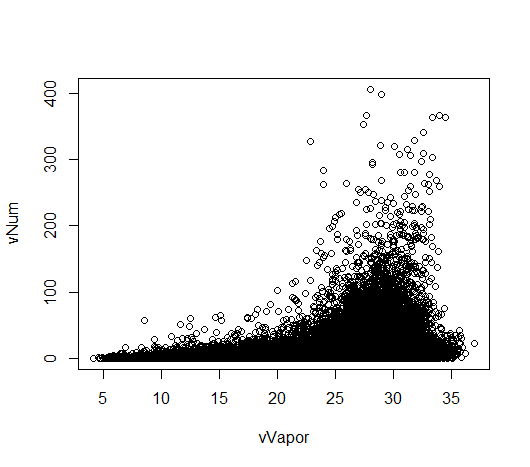
データの要約

　下記コードを実行してデータの要約を行う．

> summary(HeatStroke)

　結果は以下の通りである．

      Date                           PrefCode         Pref          
 Min.   :2008-07-01 00:00:00.00   Min.   : 1.00   Length:82785      
 1st Qu.:2012-07-18 00:00:00.00   1st Qu.:13.00   Class :character  
 Median :2015-09-17 00:00:00.00   Median :25.00   Mode  :character  
 Mean   :2015-08-29 00:12:51.26   Mean   :24.32                     
 3rd Qu.:2018-09-09 00:00:00.00   3rd Qu.:36.00                     
 Max.   :2021-09-30 00:00:00.00   Max.   :47.00                     
      Temp           Vapor         HeatStroke     
 Min.   : 8.40   Min.   : 4.20   Min.   :  0.000  
 1st Qu.:26.10   1st Qu.:19.00   1st Qu.:  1.000  
 Median :29.20   Median :23.80   Median :  2.000  
 Mean   :28.99   Mean   :23.02   Mean   :  8.171  
 3rd Qu.:32.30   3rd Qu.:27.50   3rd Qu.:  8.000  
 Max.   :40.70   Max.   :37.00   Max.   :406.000  

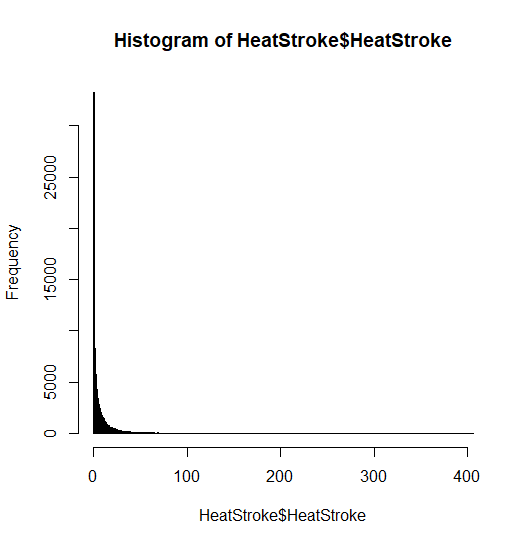
搬送人員数を図示する

　搬送人員数をヒストグラムにして分布を図示する．

> hist(HeatStroke$HeatStroke, breaks = 406)

　結果は以下の通りである．

ポアソン回帰モデルによる回帰係数の推定

　搬送人員数は非負の整数であり，下限は0であるが上限は不明であるため，まずはポアソン分布を仮定して解析してみる．

　下記を実行する．

> z = glm(vNum ~ vTemp + vVapor, family = poisson(link="log"))
> summary(z)

　結果は以下の通り．

Call:
glm(formula = vNum ~ vTemp + vVapor, family = poisson(link = "log"))

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-10.770   -1.958   -0.887    0.586   33.508  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -8.0235926  0.0142797  -561.9   <2e-16 ***
vTemp        0.2695439  0.0004490   600.3   <2e-16 ***
vVapor       0.0660829  0.0003571   185.1   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 1463940  on 82784  degrees of freedom
Residual deviance:  662439  on 82782  degrees of freedom
AIC: 879565

Number of Fisher Scoring iterations: 5

　回帰式は以下の通り．温度が1℃上昇すると搬送数が約e^0.27倍（約1.3倍）になり，平均水蒸気圧が1mmHg上昇すると搬送数が約e^0.07倍（約1.07倍）になるという意味である．

　しかし，サマリーをよく見るとResidual devianceをdegree of freedomで除した値が8.002211と1を超えており，過分散と考えられる．この場合，負の二項分布モデルを当てはめるのが妥当と考えられる．

負の二項分布モデルによる回帰係数の推定

　ポアソン回帰モデルでは過分散となったため，より分散の大きな負の二項分布モデルを適用してみる．

> y=HeatStroke$HeatStroke
> x1=HeatStroke$Temp
> x2=HeatStroke$Vapor
> library(MASS)
> Z=glm.nb(y~x1+x2)
> summary(Z)

　結果は以下の通りである．

Call:
glm.nb(formula = y ~ x1 + x2, init.theta = 1.086748839, link = log)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.6560  -1.0483  -0.4735   0.2358   5.9940  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -7.6852676  0.0329494 -233.24   <2e-16 ***
x1           0.2844962  0.0013080  217.50   <2e-16 ***
x2           0.0342140  0.0009293   36.82   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for Negative Binomial(1.0867) family taken to be 1)

    Null deviance: 193086  on 82784  degrees of freedom
Residual deviance:  89163  on 82782  degrees of freedom
AIC: 425939

Number of Fisher Scoring iterations: 1


              Theta:  1.08675 
          Std. Err.:  0.00720 

 2 x log-likelihood:  -425930.92800 

　回帰係数は若干変化しているがほぼ変わらず，AICが879565から425939に減少し，当てはまりが大きく改善されたことがわかる．

まとめ

　SQL Serverから抽出したデータをもとにRでポアソン回帰モデルおよび負の二項分布モデルを用いて日最高気温と平均水蒸気圧との回帰係数を推定した．ポアソン回帰モデルでは過分散であり，負の二項分布モデルを当てはめるのが妥当である．