空間統計を勉強している.空間相関を考慮した一般化線形モデルが地域ごとのカウントデータやバイナリーデータをモデル化するために提案されている.今回はCARモデルを扱う.CARBayesでは空間相関を考慮しない通常のポアソン回帰モデルも扱えたため備忘録として公開する.
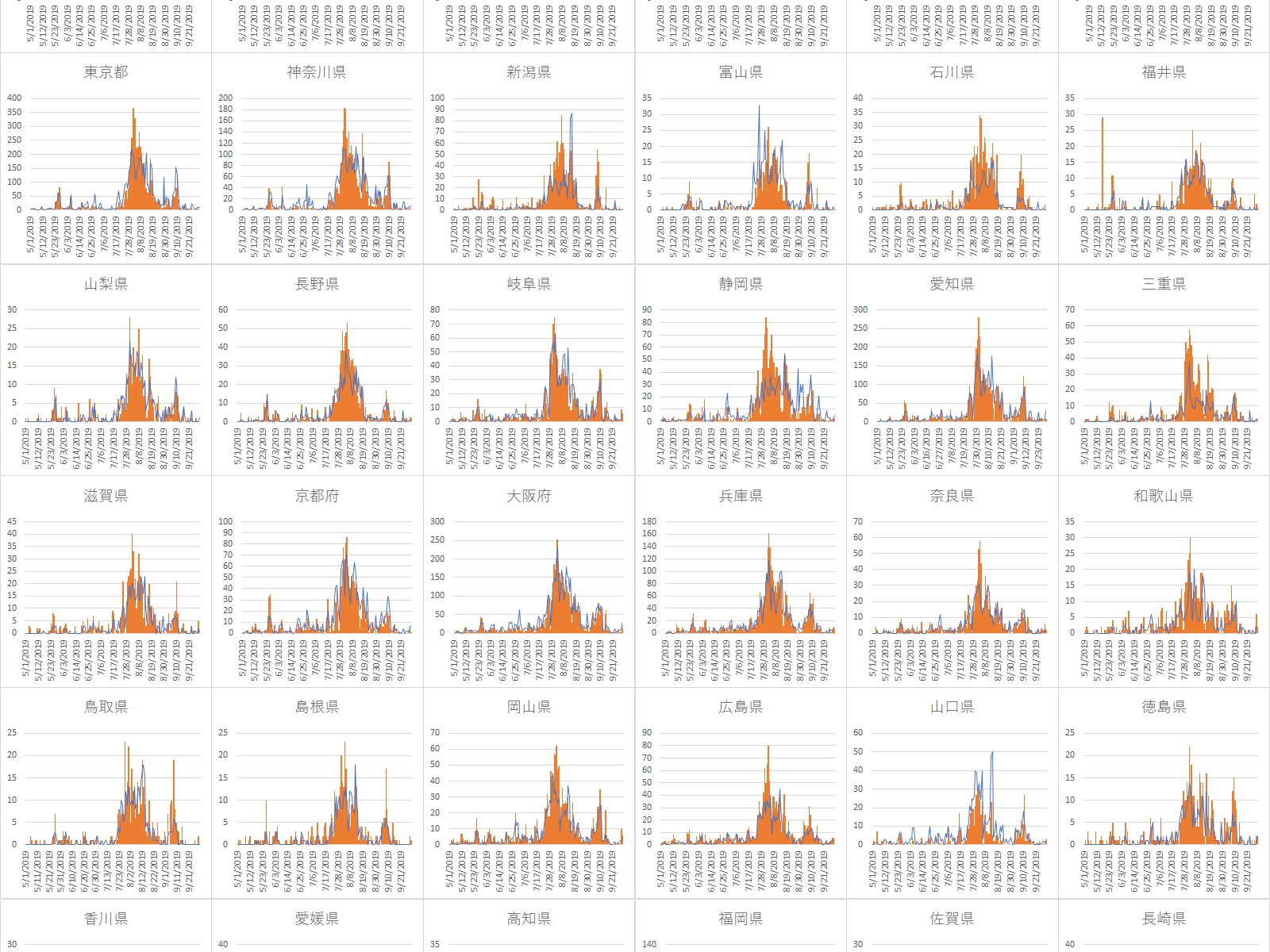
2019年の熱中症搬送人員数の予測と実際をEXCELの組み合わせグラフで描く
これまでの記事で日最高気温と平均水蒸気圧,各都道府県65歳以上人口および月から熱中症の搬送人員数を予測する回帰式の回帰係数を推定してきた.
今回はその回帰式を元に実際のデータと比較してみたい.対象は2019年の47都道府県とする.
暑熱馴化を考慮して熱中症搬送人員数を予測するモデルを構築する
人体には暑熱馴化という機構がある.暑さに体が慣れることである.この機構を取り込んだモデルを構築してみた.
熱中症搬送人員数に平均風速や平均雲量は影響するか
熱中症搬送人員数に日最高気温と平均水蒸気圧が強く影響することは疑いの余地がない.他の気象条件として風速や雲量が負の影響をおよぼす可能性はないだろうか.言い換えると,風速が強ければ熱中症を発症する可能性が下がることは考えられないか,晴れよりも曇りや雨の日は熱中症を発症する可能性が下がることは考えられないかということである.
前回の記事で熱中症データベースに平均風速をインポートした.詳細は割愛するが,同様の手順で平均雲量のデータもインポートできる.
今回は説明変数として日最高気温,平均水蒸気圧に平均風速および平均雲量を加えて一般化線形モデルにて解析を行い,tree関数で可視化を試みた.
一般化線形混合モデルを用いて熱中症搬送人員数に対する日最高気温と平均水蒸気圧の回帰係数を推定する
総務省消防庁の公開している熱中症搬送人員数は都道府県ごとに毎日データを反復抽出しているとも言える.複数の都道府県から繰り返しデータを取るのは独立した反復ではなく,疑似反復と考えられる.このような場合,都道府県単位で差が生じると考えられ,一般化線形混合モデルを用いて回帰係数を推定する必要がある.
今回はRのglmmML()関数を用いて一般化線形混合モデルを用いた回帰係数の推定を行った.
熱中症搬送人員数に都道府県人口をオフセット項として追加し一般化線形回帰分析を行う
以前の記事ではポアソン回帰モデルおよび負の二項分布モデルを用いて熱中症搬送人員数に対する日最高気温と平均水蒸気圧の回帰係数を推定した.
人口10万人あたり何名の罹患者数,というのは割り算値である.総務省消防庁の公開している熱中症搬送人員数は都道府県ごとの搬送数であり,もともと都道府県別人口が異なるのだから搬送人員数を都道府県人口で割った割合のほうが指標として適切なのではないか,という指摘は一理ある.
しかし,割り算値ではなく実数を解析すべきである.変形した観測値を統計モデルの応答変数にするのは不必要であるばかりか,誤った結果を導きかねないからである.割り算値からは確からしさの情報が失われること,変換された値の分布が不明であることから,割り算値は避けるべきである.その代わりに割り算の分母をオフセット項として線形予測子に組み込む手法がある.
熱中症搬送人員数はカウントデータであり,その期待値は集計ゾーンの集計対象人口に依存する.都道府県人口をオフセット項とすることで,都道府県の人口規模の影響を調整した回帰分析ができる.今回は都道府県人口をオフセット項として線形予測子に組み込み,一般化線形回帰分析を行ってみた.
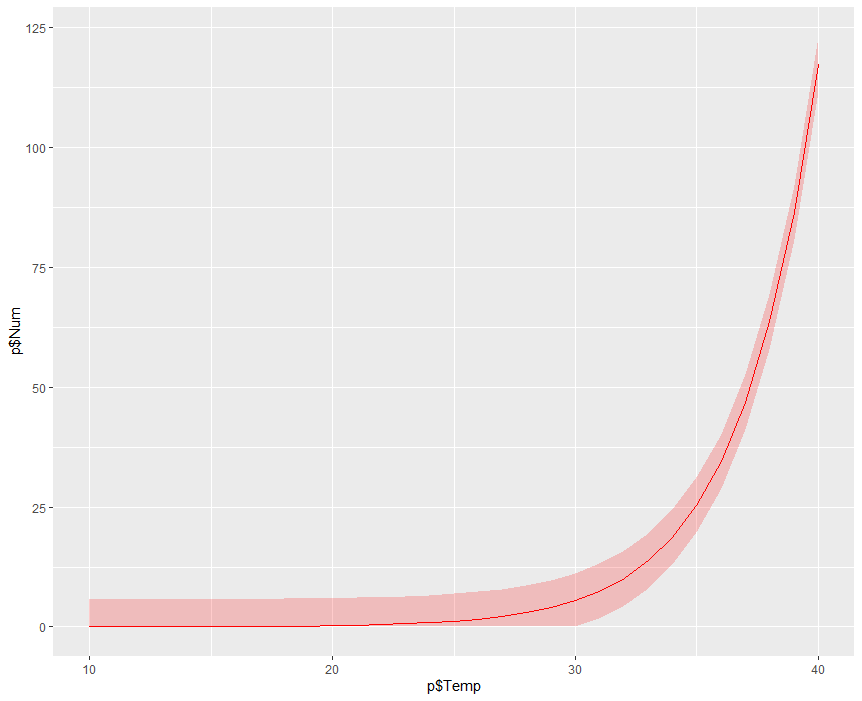
回帰曲線の95%信頼区間をRで求める
前回の記事では熱中症搬送人員数に対する日最高気温の回帰曲線を描いた.今回はポアソン分布に基づく搬送人員数の95%信頼区間を求める.
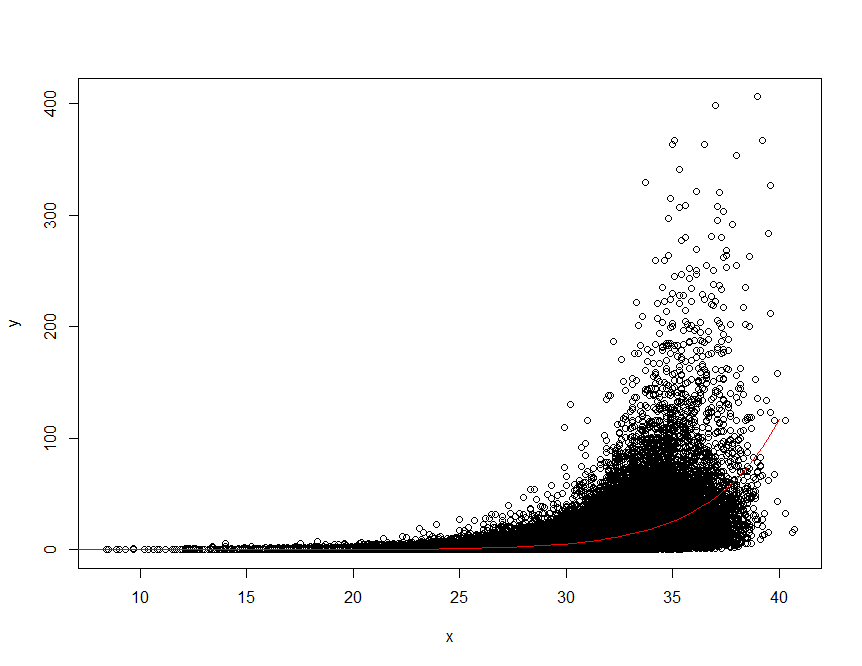
ポアソン回帰モデルの回帰曲線をRで描く
前回の記事では熱中症搬送人員数に対する日最高気温と平均水蒸気圧の影響をポアソン回帰モデルまたは負の二項分布モデルを用いて回帰係数を求めた.今回はポアソン回帰モデルの回帰曲線をRで描く.