熱中症搬送人員数に都道府県人口をオフセット項として追加し一般化線形回帰分析を行う

　以前の記事ではポアソン回帰モデルおよび負の二項分布モデルを用いて熱中症搬送人員数に対する日最高気温と平均水蒸気圧の回帰係数を推定した．

　人口10万人あたり何名の罹患者数，というのは割り算値である．総務省消防庁の公開している熱中症搬送人員数は都道府県ごとの搬送数であり，もともと都道府県別人口が異なるのだから搬送人員数を都道府県人口で割った割合のほうが指標として適切なのではないか，という指摘は一理ある．

　しかし，割り算値ではなく実数を解析すべきである．変形した観測値を統計モデルの応答変数にするのは不必要であるばかりか，誤った結果を導きかねないからである．割り算値からは確からしさの情報が失われること，変換された値の分布が不明であることから，割り算値は避けるべきである．その代わりに割り算の分母をオフセット項として線形予測子に組み込む手法がある．

　熱中症搬送人員数はカウントデータであり，その期待値は集計ゾーンの集計対象人口に依存する．都道府県人口をオフセット項とすることで，都道府県の人口規模の影響を調整した回帰分析ができる．今回は都道府県人口をオフセット項として線形予測子に組み込み，一般化線形回帰分析を行ってみた．

e-Statから都道府県別人口をダウンロード

　e-Statトップページから「地域」を選ぶ．

　「都道府県データ」の「データ表示」を選ぶ．

　「地域候補」で「全て選択」し「全国」を戻す．確定して次画面に進む．

　「表示項目選択」で分野を「A　人口・世帯」とし，大分類を「A1　人口の概要・構造」とし，小分類を「A11　人口」とし，「項目選択」で「A1101　総人口（人）」を選ぶ．

　「ダウンロード」をクリックする．

　「表ダウンロード」のダウンロード設定では「ヘッダの出力」を「出力する」のままとしておく．「注釈を表示する」のチェックを外し，「桁区切りを使用しない」にチェックする．下図では「特殊文字の選択」を「0（数字のゼロ）に置き換える」を選んでいるが，NULLないしはNAを選ぶべきであり，ダウンロード後に該当行を削除するのが本来である．

Power Queryで整形

　必要な列は年，都道府県コード，都道府県，人口である．列名をそれぞれFiscalYear, PrefCode, Prefecture, Populationとする．テキストファイルで保存する．ファイル名はT_Population.txtとする．

SQL Serverにインポート

　「データソース」を「Flat File Source」とし「参照…」からファイルを指定する．

　「変換先の選択」を「SQL Server Native Client 11.0」とする．

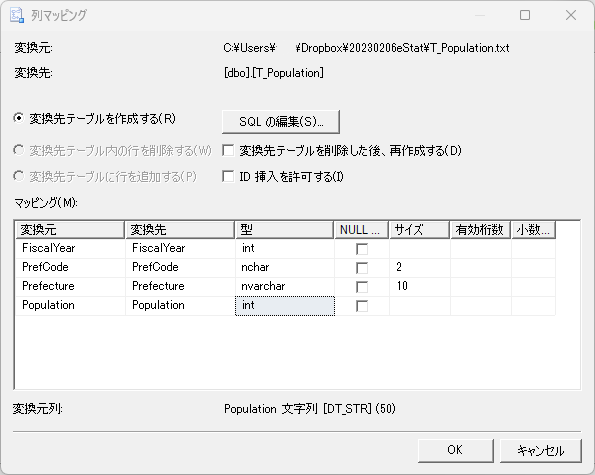
　「列マッピング」でデータ型とサイズを指定する．

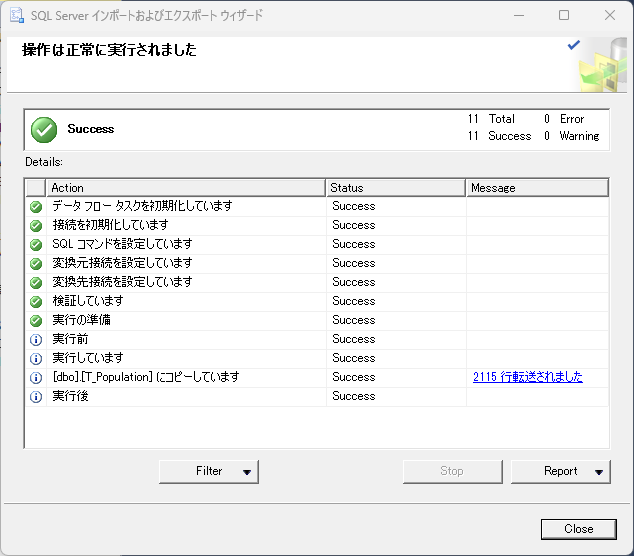
　2115行がインポートされる．

クエリでデータを抽出

　下記クエリを実行してデータを抽出する．結果をExcelにコピペして保存する．ファイル名をHeatStrokeDB.xlsxとする．

USE HeatStrokeDB;
GO
SELECT	P.PrefCode
,	P.Prefecture
,	P.FiscalYear
,	T.年月日	AS Date
,	T.日最高気温	AS Temp
,	V.日平均蒸気圧	AS Vapor
,	P.Population	AS Pop
,	H.[搬送人員（計）]	AS Num
FROM	dbo.T_HeatStroke	AS H
INNER	JOIN	dbo.T_MaxTemperature	AS T
ON	H.都道府県コード = T.都道府県コード
AND	H.日付 = T.年月日
INNER	JOIN	dbo.T_VaporPressure	AS V
ON	H.都道府県コード = V.都道府県コード
AND	H.日付 = V.年月日
INNER	JOIN	dbo.T_Population	AS P
ON	H.都道府県コード = P.PrefCode
AND	YEAR(H.日付) = P.FiscalYear
ORDER	BY	P.PrefCode, T.年月日

(70108 行処理されました)

割り算値の代わりに都道府県人口の対数をオフセット項として線形予測子に組み込む

　熱中症搬送人員数をn, 都道府県人口をNとしてポアソン分布を仮定すると，下記の式が成り立つ．

$\frac{n}{N} = Exp(\alpha + \beta_1 \times Temp + \beta_2 \times Vapor)$

　式を変形する．

$n = N \times Exp(\alpha + \beta_1 \times Temp + \beta_2 \times Vapor)$ $n = Exp(Log(N)) \times Exp(\alpha + \beta_1 \times Temp + \beta_2 \times Vapor)$ $n = Exp(\alpha + \beta_1 \times Temp + \beta_2 \times Vapor + Log(N))$

　Log(N)がオフセット項である．都道府県人口の対数を線形予測子に組み込んだ形である．

Rで一般化線形回帰分析を行う

データの読み込み，変数への代入

　下記コードを実行してHeatStrokeDB.xlsxを読み込み，変数y, x1, x2, pにそれぞれ搬送人員数，日最高気温，平均水蒸気圧，都道府県人口を代入する．

> library(readxl)
> HeatStrokeDB <- read_excel("C:/Users/***/HeatStrokeDB.xlsx", 
+     col_types = c("numeric", "text", "numeric", 
+         "date", "numeric", "numeric", "numeric", 
+         "numeric"))
> View(HeatStrokeDB)
> y = HeatStrokeDB$Num
> x1 = HeatStrokeDB$Temp
> x2 = HeatStrokeDB$Vapor
> p = HeatStrokeDB$Pop

オフセット項なしでポアソン分布を仮定する場合

　データベースが変わったため，比較を目的にベンチマークとしてオフセット項なしの一般化線形回帰分析を行う．AICは750211である．

> w = glm(y ~ x1 + x2, family = poisson(link = "log"), data = HeatStrokeDB)
> summary(w)

Call:
glm(formula = y ~ x1 + x2, family = poisson(link = "log"), data = HeatStrokeDB)
Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-10.804   -1.965   -0.891    0.596   33.428  
Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -8.1341526  0.0158004  -514.8   <2e-16 ***
x1           0.2707915  0.0004953   546.8   <2e-16 ***
x2           0.0685135  0.0003906   175.4   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
    Null deviance: 1243632  on 70107  degrees of freedom
Residual deviance:  567265  on 70105  degrees of freedom
AIC: 750211
Number of Fisher Scoring iterations: 5

オフセット項ありでポアソン分布を仮定する場合

　都道府県人口の対数をオフセット項として追加し，一般化線形回帰分析を行う．AICは480515に改善している．

> z = glm(y ~ x1 + x2, offset = log(p), family = poisson(link = "log"), data = HeatStrokeDB)
> summary(z)

Call:
glm(formula = y ~ x1 + x2, family = poisson(link = "log"), data = HeatStrokeDB, 
    offset = log(p))
Deviance Residuals: 
     Min        1Q    Median        3Q       Max  
-13.0022   -1.2911   -0.4225    0.9607   19.7591  
Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -2.293e+01  1.570e-02 -1460.9   <2e-16 ***
x1           2.730e-01  5.034e-04   542.3   <2e-16 ***
x2           6.671e-02  3.987e-04   167.3   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
    Null deviance: 984714  on 70107  degrees of freedom
Residual deviance: 297569  on 70105  degrees of freedom
AIC: 480515
Number of Fisher Scoring iterations: 5

オフセット項なしで負の二項分布を仮定する場合

　さらに欲張って負の二項分布を仮定してみる．AICは360530とポアソン分布よりも予測性能が高い．

> y = HeatStrokeDB$Num
> x1 = HeatStrokeDB$Temp
> x2 = HeatStrokeDB$Vapor
> p = HeatStrokeDB$Pop
> z = glm.nb(y ~ x1 + x2, data = HeatStrokeDB)
> summary(z)

Call:
glm.nb(formula = y ~ x1 + x2, data = HeatStrokeDB, init.theta = 1.057957391, 
    link = log)
Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.6241  -1.0533  -0.4774   0.2303   5.9534  
Coefficients:
             Estimate Std. Error z value Pr(>|z|)    
(Intercept) -7.668407   0.036287 -211.33   <2e-16 ***
x1           0.282649   0.001444  195.76   <2e-16 ***
x2           0.035372   0.001020   34.69   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for Negative Binomial(1.058) family taken to be 1)
    Null deviance: 161258  on 70107  degrees of freedom
Residual deviance:  75571  on 70105  degrees of freedom
AIC: 360530
Number of Fisher Scoring iterations: 1
              Theta:  1.05796 
          Std. Err.:  0.00760 
 2 x log-likelihood:  -360521.83600

オフセット項ありで負の二項分布を仮定する場合

　都道府県人口の対数をオフセット項として線形予測子に組み込んだ場合はどうだろうか．AICは5265246と大幅に悪化した．

> w = glm.nb(y ~ x1 + x2, offset(log(p)), data = HeatStrokeDB)
> summary(w)

Call:
glm.nb(formula = y ~ x1 + x2, data = HeatStrokeDB, weights = offset(log(p)), 
    init.theta = 1.052690849, link = log)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-9.8194  -4.0229  -1.8965   0.7493  22.9171  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept) -7.6644546  0.0095107  -805.9   <2e-16 ***
x1           0.2836617  0.0003792   748.0   <2e-16 ***
x2           0.0354114  0.0002681   132.1   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for Negative Binomial(1.0527) family taken to be 1)

    Null deviance: 2344047  on 70107  degrees of freedom
Residual deviance: 1093700  on 70105  degrees of freedom
AIC: 5265246

Number of Fisher Scoring iterations: 1


              Theta:  1.05269 
          Std. Err.:  0.00197 

 2 x log-likelihood:  -5265238.35100

結果

　ポアソン分布を仮定した場合，都道府県人口の対数をオフセット項として追加したほうが予測性能が改善する可能性がある．負の二項分布を仮定するとさらに予測性能が改善する可能性があるが，都道府県人口をオフセット項として追加すると逆に予測性能が低下した．